pnorm(0)[1] 0.5Normal ve Diğer Dağılımlar: R Uygulamaları
Olasılık Yoğunluk Fonksiyonları
Bir z Değeri İçin Kümülatif Olasılık: pnorm()
z Değerleri ve Kritik Değerler
qnorm(c(0.025, 0.975)) # %95 güven aralığı[1] -1.959964 1.959964round(qnorm(c(0.005, 0.995)), 2) # %99 güven aralığı[1] -2.58 2.58Yüzdelik Değerler İçin z Değeri: qnorm()
qnorm(0.50)[1] 0qnorm(c(0.025, 0.975)) # Güven aralığı[1] -1.959964 1.959964Rastgele Değer Üretme: rnorm()
rnorm(10, mean = 0, sd = 1) [1] 0.6671321 -0.6628779 0.8731343 -1.5352241 -0.2164052 -0.8699757
[7] -0.1623740 0.3751100 -0.8179061 0.3799156Binom Dağılımı: dbinom()
Bu deneyde, her X = k değeri için olasılık Binom Dağılımı kullanılarak hesaplanır:
\[P(X = k) = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}\]
Burada: - n = 2: Deneme sayısı,
k : Başarı sayısı,
p = 0.5 : Başarı olasılığı.
Aşağıda her bir k için olasılık hesaplamaları gösterilmiştir:
\[ P(X = 0) = \binom{2}{0} \cdot 0.5^0 \cdot 0.5^2 = 1 \cdot 1 \cdot 0.25 = 0.25 \] \[ P(X = 1) = \binom{2}{1} \cdot 0.5^1 \cdot 0.5^1 = 2 \cdot 0.5 \cdot 0.5 = 0.5 \]
\[ P(X = 2) = \binom{2}{2} \cdot 0.5^2 \cdot 0.5^0 = 1 \cdot 0.25 \cdot 1 = 0.25 \]
Aşağıdaki R kodu, olasılıkları görselleştirmek için bir çubuk grafik oluşturur:
Bozuk Para Örneği
Bozuk parayı iki kez attığınızda olasılık dağılımı:
x <- 0:2
plot(x, dbinom(x, size = 2, p = 0.5),
type = "h", col = "red",
lwd = 10,
main = "Bozuk Parayı İki Kere Havaya Atma")
# YY
# TT
# YT
# TYBinom Dağılımı İçin Daha Büyük Örnekler
x <- 0:30
plot(x, dbinom(x, size = 30, p = 0.5),
type = "h",
main="n=30 için Binom Dağılımı")
Deney, birbirinden bağımsız ve iki olasılık durumuna (başarı ya da başarısızlık) sahip denemeler içeriyor. 𝑛=30 𝑝= 0.5
p=0.5: Her bir denemenin başarı olasılığı (örneğin, yazı gelmesi). Bu, bir madeni parayı 30 kez havaya atmak gibi ideal bir durum için geçerlidir; ama sadece madeni para atmayı değil, aşağıdaki gibi başka durumları da temsil edebilir:
Hastaların iyileşme olasılığı: 30 hasta üzerinde yapılan bir deneyde her hastanın iyileşme olasılığı %50 ise, kaçının iyileşebileceğini modellemek.
Doğru cevap verme olasılığı: Bir sınavda rastgele şık seçen bir öğrencinin doğru p=0.5 olduğunda, 30 soruda kaç doğru yapabileceği.
Başarıyı ölçen diğer deneyler: Örneğin, 30 müşteriden kaçının bir ürünü satın almayı tercih edeceği, başarı olasılığının olduğu bir durum.
Normal Dağılım: Yoğunluk ve Yığılma
Yoğunluk Dağılımı
x <- seq(-4, 4, 0.01)
plot(x, dnorm(x),
type = "l",
main = "Normal Dağılım Yoğunluk Fonksiyonu")
Yığılma Dağılımı
plot(x, pnorm(x), type = "l",
main = "Normal Dağılım Yığılım Fonksiyonu")
Merkezi limit teoremi
IQ gibi gerçek hayat verilerinde normal dağılımın kullanımı:
IQ <- seq(55, 145, 0.1)
plot(IQ, dnorm(IQ, mean = 100, sd = 15), type = "l")
abline(v = 100, col = "red")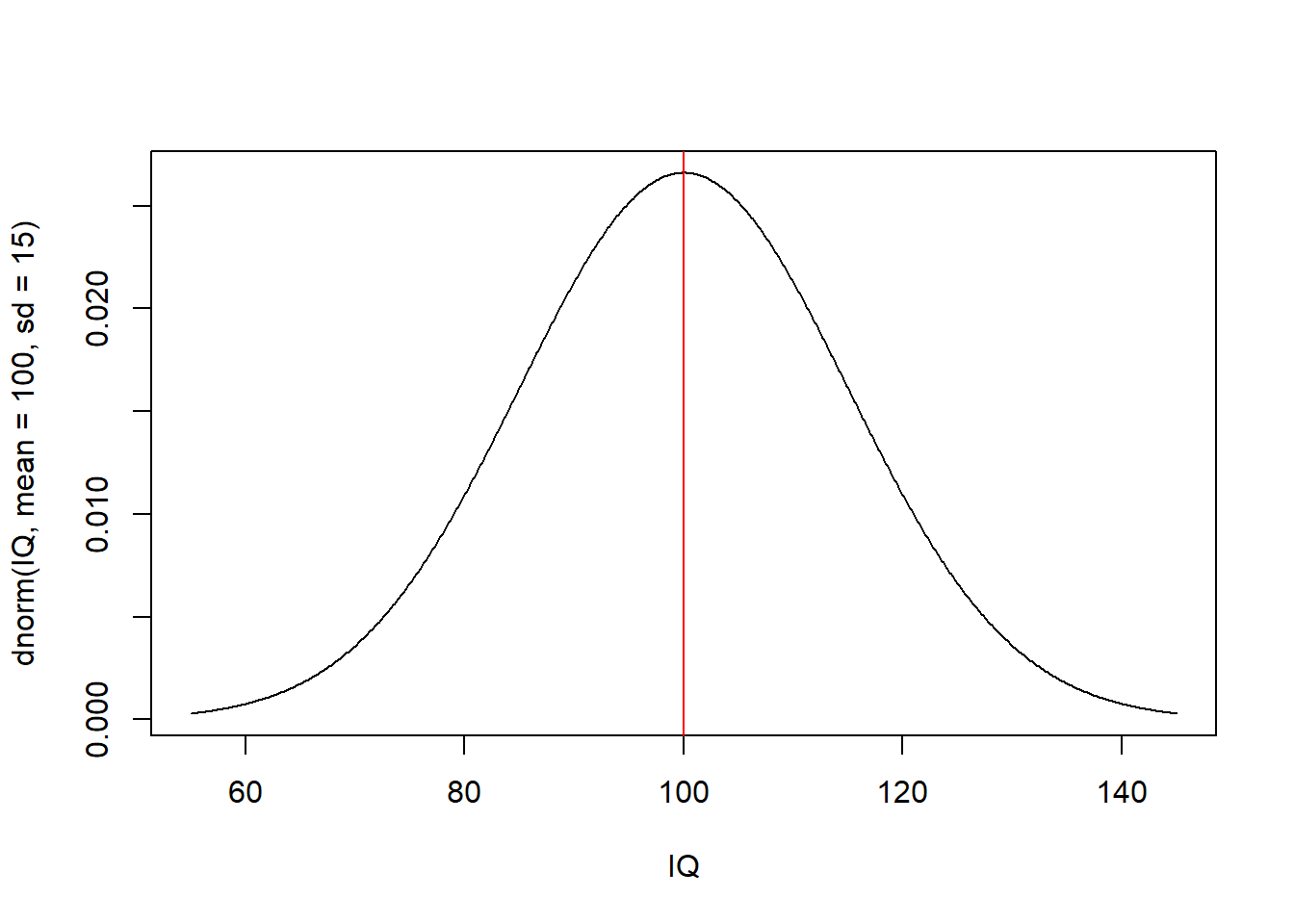
Merkezi Limit Teoremi
Örneklem büyüklüğü arttıkça dağılımın nasıl daraldığını inceleyelim.
3 Kişilik Örneklem
sample_means <- replicate(1000,
mean(rnorm(3, mean = 100, sd = 15)))
hist(sample_means,
main = "3 Kişilik Örneklem Ortalamaları",
col = "skyblue")
30 Kişilik Örneklem
sample_means <- replicate(1000,
mean(rnorm(30, mean = 100, sd = 15)))
hist(sample_means,
main = "30 Kişilik Örneklem Ortalamaları",
col = "lightgreen")
Örnekleme Dağılımı
Seçkisiz bir örneklem için hesaplanmış bir istatistik aslında bir değişkendir ve belli bir dağılıma sahiptir. Örnekleme dağılım konusunu açıklamak için en çok kullanılan istatistik aritmetik ortalamadır.
Merkezi Limit Teoremi’ne göre, basit seçkisiz örneklem kullanıldığında değişkenin evrende gösterdiği dağılımdan bağımsız olarak, o değişkene ait örneklem ortalamalarının dağılımı yaklaşık olarak normaldir.
Bu bölümde, örnekleme dağılımlarının histogramını ve Q-Q grafiğini çizeceğiz. Q-Q grafiği, kuramsal normal dağılım değerleri ile gerçek değerler arasındaki ilişkiyi gösterir. Oluşan doğrunun eğimi 45 dereceye yaklaştığında normal dağılıma yakınlık artar.
Küçük ve Büyük Örneklem Boyutları İçin Örnekleme Dağılımları
nreps <- 10000
nsmall <- 2
nlarge <- 30
sampdist.mean.small <- numeric(nreps)
sampdist.mean.large <- numeric(nreps)
# Küçük örneklem büyüklüğü için
par(mfrow = c(2,2))
for (i in 1:nreps) {
sample <- runif(nsmall, 0, 100)
sampdist.mean.small[i] <- mean(sample)
}
# Histogram çizme
hist(sampdist.mean.small,
main = "Küçük Örneklem Ortalamalarının \n Dağılımı (n = 2)",
xlab = "Örneklem Ortalamaları",
col = "lightblue")
# Q-Q grafiği
qqnorm(sampdist.mean.small,
main = "Q-Q Grafiği: Küçük Örneklem (n = 2)")
qqline(sampdist.mean.small, col = "red")
# Büyük örneklem büyüklüğü için
for (i in 1:nreps) {
sample <- runif(nlarge, 0, 100)
sampdist.mean.large[i] <- mean(sample)
}
# Histogram çizme
hist(sampdist.mean.large,
main = "Büyük Örneklem Ortalamalarının \n Dağılımı (n = 30)",
xlab = "Örneklem Ortalamaları",
col = "lightgreen")
# Q-Q grafiği
qqnorm(sampdist.mean.large,
main = "Q-Q Grafiği: Büyük Örneklem (n = 30)")
qqline(sampdist.mean.large, col = "blue")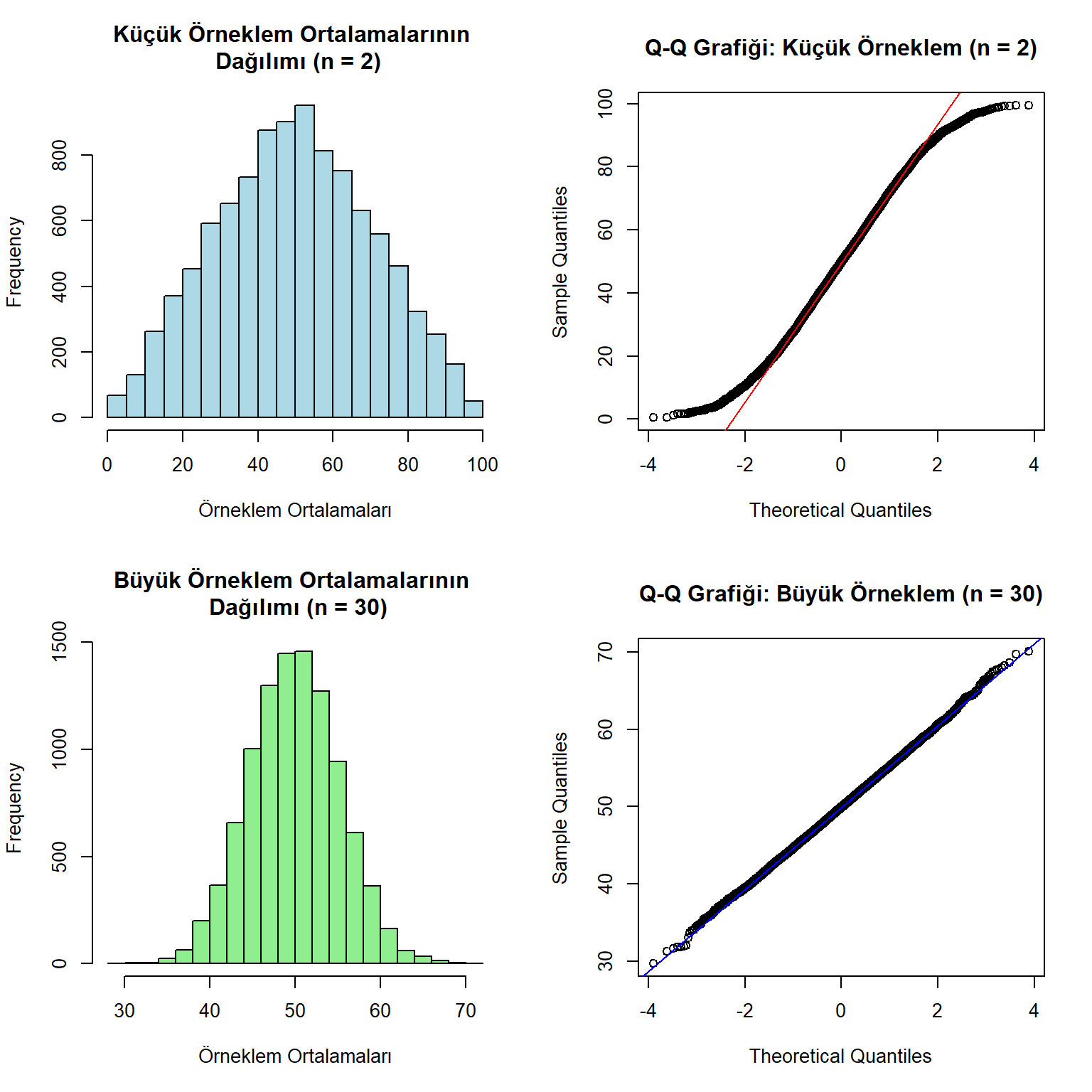
Bu grafikler, örneklem boyutunun artmasıyla birlikte dağılımın normal dağılıma daha çok yaklaştığını göstermektedir.
Uniform Dağılım Örneği
uniform_samples <- runif(1000, min = 0, max = 10)
hist(uniform_samples,
main = "Uniform Dağılım", col = "orange")
T Dağılımı: dt()
curve(dt(x, df = 10),
from = -4, to = 4, main = "t Dağılımı")
Poisson Dağılımı: dpois()
x <- 0:10
plot(x, dpois(x, lambda = 3),
type = "h", main = "Poisson Dağılımı")
Ki-Kare Dağılımı: dchisq()
curve(dchisq(x, df = 5), from = 0, to = 20,
main = "Ki-Kare Dağılımı")
Sonuç
Bu derste normal dağılım başta olmak üzere binom, t, Poisson, ve ki-kare dağılımlarını tanıdık. Her bir dağılımın kendine özgü uygulamaları ve görselleştirmeleri bulunmaktadır. Merkezi Limit Teoremi ve dağılımların istatistiksel analizlerdeki önemini vurguladık.