Hipotez Testleri

Hipotez Testleri

Hipotez testi, belirli bir iddianın (hipotezin) doğru olup olmadığını test etmek için kullanılan bir istatistiksel yöntemdir. Araştırmacılar, hipotez testlerini genellikle anlamlılık düzeyleri (alfa düzeyi) ile değerlendirir.

Problem: 2 yaşındaki bebeklerin ağırlığı \(\mu=13\) kg ve \(\sigma=2\) kg olan normal bir dağılım oluşturmaktadır. Araştırmacılar, temas yoluyla (dokunma, kucaklama gibi) bebeklerin gelişiminin hızlanabileceği tezini test etmek istemektedir. Bu amaçla \(n=16\) olan yeni doğmuş bebeklerden bir örneklem oluşturulmuş ve aileleri, bebeklerine nasıl temas etmeleri gerektiği konusunda bilgilendirilmiştir. Bebekler 2 yaşına geldiğinde ağırlıkları ölçülmüş ve ortalama hesaplanmıştır. Şu durumlar değerlendirilir:

  • Eğer ortalama \(\mu=13\) kg’dan oldukça yüksekse, araştırmacılar temasın bebeğin gelişimini hızlandırdığı sonucuna varacaktır.
  • Eğer ortalama \(\mu = 13\) kg civarındaysa, temasın bebeklerin gelişimini hızlandırdığına dair bir kanıt olmadığı sonucuna varılacaktır.

Hipotezler

  • \(H_0: \mu_{temas}=13\) kg (Temas edilen bebekler için ağırlık ortalaması 13’tür.)
  • \(H_1: \mu \neq 13\) kg (Temas edilen bebekler için ağırlık ortalaması 13 değildir.)

Alfa düzeyi (\(\alpha\)), sıfır hipotezinin doğru olduğu durumlarda düşük olasılıklı örneklemleri belirtmek için kullanılan bir olasılık değeridir. Yaygın olarak kullanılan alfa değerleri şunlardır:

  • \(\alpha=0.05\) (%5),
  • \(\alpha=0.01\) (%1),
  • \(\alpha=0.001\) (%0.1).

Alfa düzeyi ile belirlenen uç değerlerin oluşturduğu bölgeye kritik bölge denir. Eğer araştırma sonucunda elde edilen değerler kritik bölgede konumlanıyorsa, sıfır hipotezi reddedilir.

I. Tip hata, sıfır hipotezinin doğru olduğu halde reddedilmesi durumunda ortaya çıkar. Yani:

  • Gerçekte bir etkisi olmayan bir uygulamanın etkisi olduğu sonucuna varılır.

II. Tip hata, gerçekte yanlış olan bir sıfır hipotezinin reddedilmemesi durumunda ortaya çıkar. Bu durumda:

  • Uygulamanın etkisi olduğu halde, bu etki hipotez testi ile ortaya çıkarılamaz.

Örnek 1: Bebeklerin Ağırlığı

  • 2 yaşındaki bebeklerin ağırlıklarının \(\mu=13\) kg ve \(\sigma=4\) kg olduğu bilinmektedir. Araştırmacılar \(n=16\) olan yeni doğmuş bebeklerden bir örneklem seçmiştir. Bebekler 2 yaşına geldiğinde ağırlıkları ölçülmüş ve ortalama \(\bar{X}=16.5\) kg bulunmuştur.

Hipotezler

  • Yönsüz:
    • \(H_0: \mu=13\)
    • \(H_1: \mu \neq 13\)
sd <- 4
M <- 13
X <- 16.5
n <- 16
sd_hata <- sd / sqrt(n)
z <- (X - M) / sd_hata
z
[1] 3.5
qnorm(c(0.025, 0.975)) # Kritik değerler
[1] -1.959964  1.959964
  • Yönlü:
    • \(H_0: \mu \leq 13\)
    • \(H_1: \mu > 13\)
qnorm(0.95) # Yönlü kritik değer
[1] 1.644854

Örnek 2: Uygulama Etkisi

Bir popülasyonun normal dağılıma sahip olduğu ve \(\mu=80\), \(\sigma=10\) olduğu bilinmektedir. Bu popülasyondan \(n=25\) olan bir örneklem seçilmiş ve uygulama sonunda \(\bar{X}=81\) bulunmuştur. \(\alpha=0.05\) iken uygulamanın etkisi test edilmiştir.

M <- 80
sd <- 10
n <- 25
X <- 81
sd_hata <- sd / sqrt(n)
z <- (X - M) / sd_hata
z
[1] 0.5
qnorm(c(0.025, 0.975)) # Kritik değerler
[1] -1.959964  1.959964

Kritik bölgenin sınırı \(z=1.96\) ise:

\(H_0\) reddedilemez.

Eğer \(n=400\) olsaydı:

n <- 400
sd_hata <- sd / sqrt(n)
z <- (X - M) / sd_hata
z
[1] 2
qnorm(c(0.025, 0.975))
[1] -1.959964  1.959964

Neden Hipotez Testleri

En soyut haliyle hipotez testinin çok basit bir mantığı vardır: Araştırmacının dünya hakkında bir teorisi vardır ve verilerin bu teoriyi gerçekten destekleyip desteklemediğini belirlemek ister. Hipotez testinde amaç

  • Bir modeldeki parametrelerin belirli değerler alıp almadığını veya belirli aralıklara düşüp düşmediğini araştırmak önemli farklılıkları veya tesadüfen oluşmayan farklılıkları tespit etmektir.

Bu hedeflere ulaşmak için, bir popülasyon hakkında birbiriyle rekabet eden iki hipotez arasında karar vermemize yardımcı olması amacıyla bir örneklemden elde edilen verileri kullanacağız. Bu iki tamamlayıcı hipotez şunlardır:

  • \(H_0\) kanıtlamak istediğimiz şeyin tam tersine karşılık gelir
  • \(H_1\) gerçekte neye inandığımızı temsil eder.

Önemli bir kanıt aradığımız iddia, alternatif hipoteze atanır. Alternatif genellikle araştırmacının ortaya koymak ya da kanıt bulmak istediği şeydir. Genellikle yokluk hipotezi, gerçekten “etki yok” veya “fark yok” iddiasıdır. Çoğu durumda, sıfır hipotezi ilginç bir şey olmadığını temsil eder.

Örnek: Havalimanı Güvenlik Kontrolü

  • Sıfır Hipotezi (H₀): Yolcunun çantasında tehlikeli bir madde yok.

  • Alternatif Hipotez (H₁): Yolcunun çantasında tehlikeli bir madde var.

Süreç:

  • Varsayılan Durum: Güvenlik kontrolüne gelen her yolcunun çantasında başlangıçta tehlikeli bir madde olmadığı varsayılır. Bu, sıfır hipotezine karşılık gelir.

  • Kanıt Arama: X-ray cihazı çantayı tarar ve elde edilen görüntü, çantada şüpheli bir nesne olup olmadığını belirlemek için incelenir.

Karar:

  • Eğer X-ray taramasında çantada şüpheli bir nesne tespit edilmezse, sıfır hipotezi kabul edilir (yolcunun çantasında tehlikeli bir madde olmadığı sonucuna varılır).

  • Eğer X-ray cihazı şüpheli bir nesne tespit ederse, bu sıfır hipotezine karşı güçlü bir kanıt oluşturur. Bu durumda güvenlik görevlileri çantayı daha ayrıntılı bir şekilde arar (sıfır hipotezi reddedilir).

Sonuç:

  • Tehlikeli bir nesne bulunamazsa, yolcunun çantasının güvenli olduğu varsayımı korunur.

  • Tehlikeli bir nesne bulunursa, bu, alternatif hipotezin doğru olduğunu (çantada tehlikeli madde olduğunu) gösterir.

Örnek: Hırsızlık Davası

Bir hırsızlık davasını ele alalım. İki Çelişkili İddia:

  • Savcı: Suçlanan kişinin hırsızlık yaptığına dair bir iddiada bulunur.

  • Sanık: Hırsızlık yapmadığını savunur.

Başlangıç Varsayımı:

  • Hukuk kurallarına göre, suçlanan kişi başlangıçta masum olarak kabul edilir. Bu, hipotez testindeki sıfır hipotezine (H₀) denk gelir: “Sanık suçsuzdur.”

Kanıt Sunma ve İspat:

  • Savcı, sanığın suçlu olduğunu göstermek için kanıtlar sunar. Bu kanıtlar, güvenlik kameraları, tanık ifadeleri veya çalıntı eşyalar gibi çeşitli kaynaklardan gelebilir. Ancak bu kanıtların sanığın suçlu olduğunu “şüpheye yer bırakmayacak şekilde” göstermesi gerekir.

Karar Süreci:

  • Eğer sunulan kanıtlar, sanığın suçlu olduğunu gösteremeyecek kadar zayıfsa, mahkeme “suçsuzdur” sonucuna varır. Bu durumda sıfır hipotezi reddedilmez. Eğer kanıtlar çok güçlü ve netse, mahkeme sıfır hipotezini reddeder ve “suçludur” kararı verir.

“Suçsuz” İle “Masum” Ayrımı:

  • Mahkeme asla “Sanık kesinlikle masumdur” demez. Çünkü mahkeme sadece elde edilen kanıtlara dayanarak karar verir. “Sanık suçsuzdur” demek, yalnızca suçlu olduğuna dair yeterince güçlü kanıt olmadığını ifade eder.

  • Hipotez testinde de durum aynıdır: Sıfır hipotezi reddedilmezse, bu hipotezin doğru olduğu anlamına gelmez. Sadece onu çürütecek yeterli kanıt bulunmadığı anlamına gelir.

  • Tıpkı bir ceza davasında olduğu gibi, hipotez testinde de bir varsayımı çürütmek için güçlü ve güvenilir kanıtlara ihtiyaç duyulur. Kanıtların yetersiz olması durumunda, mevcut varsayım (sıfır hipotezi) korunur, ancak bu varsayımın mutlak doğru olduğu sonucuna varılmaz.

Çıkarımsal İstatistik

Bir örneklemin, belirli bir popülasyona ait olup olmadığını test etmek için kullanılan bir yöntemdir. z testi için:

  • Veri en az eşit aralık ölçeğinde olmalıdır.
  • Popülasyon normal dağılıma sahip olmalıdır.
  • Popülasyonun ortalaması ve standart sapması bilinmelidir.

t testi, popülasyonun standart sapması bilinmediğinde örneklem standart sapmasının kullanıldığı bir testtir. 1908’de William Gosset tarafından geliştirilmiştir.

  • t dağılımının şekli serbestlik derecesine bağlıdır.

  • Serbestlik derecesi arttıkça dağılım normalleşir.

  • tek örneklem t testi Bir örnek ortalamasının belirli bir değere eşit olup olmadığını test etmek için:

    • \(H₀ : \mu = \text{deger}\)

  • İki örneklem t testi

İki örnek ortalamasının eşit olup olmadığını test etmek için:

-  Bağımsız örneklem t testi  $H₀ :  \mu_1 = \mu_2$
-  Bağımlı örneklem t testi  $H₀ :  \mu_D = 0$

  • ANOVA

    • Üç veya daha fazla grup ortalamasının eşit olup olmadığını test etmek için: \(H₀ : \mu_1 = \mu_2 = \mu_3 = = \mu_4 ...== \mu_k\)

Tek Örneklem t Testi

Bir veri seti kullanarak, popülasyon ortalamasını (μ) test etmek istediğimizi varsayalım. Veri seti büyüklüğü (n) biliniyor ancak popülasyon standart sapması (σ) bilinmiyor.
Bu durumda, sıfır hipotezini \(H_0: \mu = \mu_0\) bazı alternatif hipotezlere karşı, anlamlılık düzeyi \(\alpha\) ile test etmek istiyoruz.

Test istatistiği şu şekilde hesaplanır:

\(t = \frac{\bar{X} - \mu_0}{s / \sqrt{n}}\)

Burada serbestlik derecesi df = n - 1 olarak hesaplanır.

Formüldeki değişkenler:

  • \(\bar{X}\): Örneklem ortalaması
  • \(\mu_0\): Karşılaştırmak istediğimiz popülasyon ortalaması
  • \(s\): Örneklem standart sapması
  • \(n\): Örneklem büyüklüğü

Karar verme süreci:

  • Eğer \(t > t_{\text{kritik}}\) ise \(\alpha\) anlamlılık düzeyinde, sıfır hipotezini reddederiz.

  • Aksi halde, sıfır hipotezini reddetmeyiz.

Tek Örneklem t-testi uygulama

Tek örneklem t-testi, bir örneklem ortalamasının belirli bir değerden farklı olup olmadığını test eder.

Örnek veri oluşturma

set.seed(123)
data <- rnorm(100, mean = 52, sd = 5)

t-testi uygulama

t_test_result <- t.test(data, mu = 50)

Sonuçları gösterme

t_test_result

    One Sample t-test

data:  data
t = 5.3725, df = 99, p-value = 5.159e-07
alternative hypothesis: true mean is not equal to 50
95 percent confidence interval:
 51.54642 53.35764
sample estimates:
mean of x 
 52.45203

Sonuçları daha okunaklı bir tablo halinde sunalım:

library(knitr)
library(dplyr)
library(kableExtra)
t_test_table <- data.frame( İstatistik = c("t-değeri", 
              "Serbestlik Derecesi", "p-değeri", "
              Güven Aralığı", "Örneklem Ortalaması"), 
                Deger = c( round(t_test_result$statistic, 3),
                t_test_result$parameter, 
                round(t_test_result$p.value, 4),
                paste(round(t_test_result$conf.int, 2),
                   collapse = " - "), 
                  round(t_test_result$estimate, 2) ) )

kable(t_test_table, caption = "Tek Örneklem T-testi Sonuçları") %>%
  kable_styling(bootstrap_options = c("striped", "hover"))
Tek Örneklem T-testi Sonuçları
İstatistik Deger
t-değeri 5.372
Serbestlik Derecesi 99
p-değeri 0
Güven Aralığı 51.55 - 53.36
Örneklem Ortalaması 52.45

lsr paketi aynı analizi yapar ve daha düzenli çıktılar sağlar:

library("lsr")

# Run one-sample t test
oneSampleTTest(x=data, mu=50, conf.level=0.95, one.sided=FALSE)

   One sample t-test 

Data variable:   data 

Descriptive statistics: 
              data
   mean     52.452
   std dev.  4.564

Hypotheses: 
   null:        population mean equals 50 
   alternative: population mean not equal to 50 

Test results: 
   t-statistic:  5.372 
   degrees of freedom:  99 
   p-value:  <.001 

Other information: 
   two-sided 95% confidence interval:  [51.546, 53.358] 
   estimated effect size (Cohen's d):  0.537

α=.05 anlamlılık seviyesi ile ortalamanın 50 olduğu Ho hipotezini reddediyoruz,\(t_{(99)}=5.372 ,p<.001 ,CI95=[51.546, 53.358]\) .

Bağımsız Örneklem t Testi

İki bağımsız popülasyondan veri topladığımızı varsayalım:
\(x_1 \sim N(\mu_{x_1}, \sigma_{x_1})\) ve \(x_2 \sim N(\mu_{x_2}, \sigma_{x_2})\).
Bu durumda, iki popülasyon ortalamasının \(\mu_{x_1}\) ve \(\mu_{x_2}\) eşit olup olmadığını test etmek istiyoruz.

Sıfır hipotezi: \(H_0: \mu_{x_1} = \mu_{x_2}\)

Alternatif hipotez: \(H_A: \mu_{x_1} \neq \mu_{x_2}\)

Anlamlılık düzeyi: \(\alpha\)

Test istatistiği aşağıdaki formülle hesaplanır:

\(t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{s_p^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}}\)

Burada, \(s_p\) birleşik varyanstır ve şu şekilde hesaplanır:

\(s_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}\)

Serbestlik derecesi df şu şekilde hesaplanır:

\(df = n_1 + n_2 - 2\)

  • \(\bar{X}_1\) İlk grubun örneklem ortalaması

  • \(\bar{X}_2\) İkinci grubun örneklem ortalaması

  • \(s_1^2\) İlk grubun örneklem varyansı

  • \(s_2^2\) İkinci grubun örneklem varyansı

  • \(s_p^2\) birleşik varyans

  • \(n_1\) İlk grubun örneklem büyüklüğü

  • \(n_2\) İkinci grubun örneklem büyüklüğü

  • Eğer \(t > t_{\text{kritik}}\) \(\alpha\) anlamlılık düzeyinde, sıfır hipotezini reddederiz.

  • Aksi takdirde, sıfır hipotezini reddetmeyiz.

Bağımsız Örneklem t-testi Uygulama

Bağımsız iki örneklem t-testi, iki bağımsız grubun ortalamalarını karşılaştırır.

Örnek veri oluşturma

set.seed(456)
group1 <- rnorm(50, mean = 25, sd = 5) 
group2 <- rnorm(50, mean = 28, sd = 5)

t-testi uygulama

ind_t_test <- t.test(group1, group2)

Sonuçları gösterme

ind_t_test

    Welch Two Sample t-test

data:  group1 and group2
t = -2.7148, df = 96.986, p-value = 0.00785
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -4.7291397 -0.7346981
sample estimates:
mean of x mean of y 
 25.73691  28.46883

Sonuçları daha okunaklı bir tablo halinde sunalım:

library(ggplot2)
data_long <- data.frame( value = c(group1, group2), 
                         group = rep(c("Grup 1", "Grup 2"), 
                                     each = 50) )

ggplot(data_long, aes(x = group, y = value, fill = group)) + 
  geom_boxplot() + 
  geom_jitter(width = 0.2, alpha = 0.5) + 
  theme_minimal() + 
  labs(title = "Grup 1 ve Grup 2 Karşılaştırması", x = "Gruplar", y = "Değerler")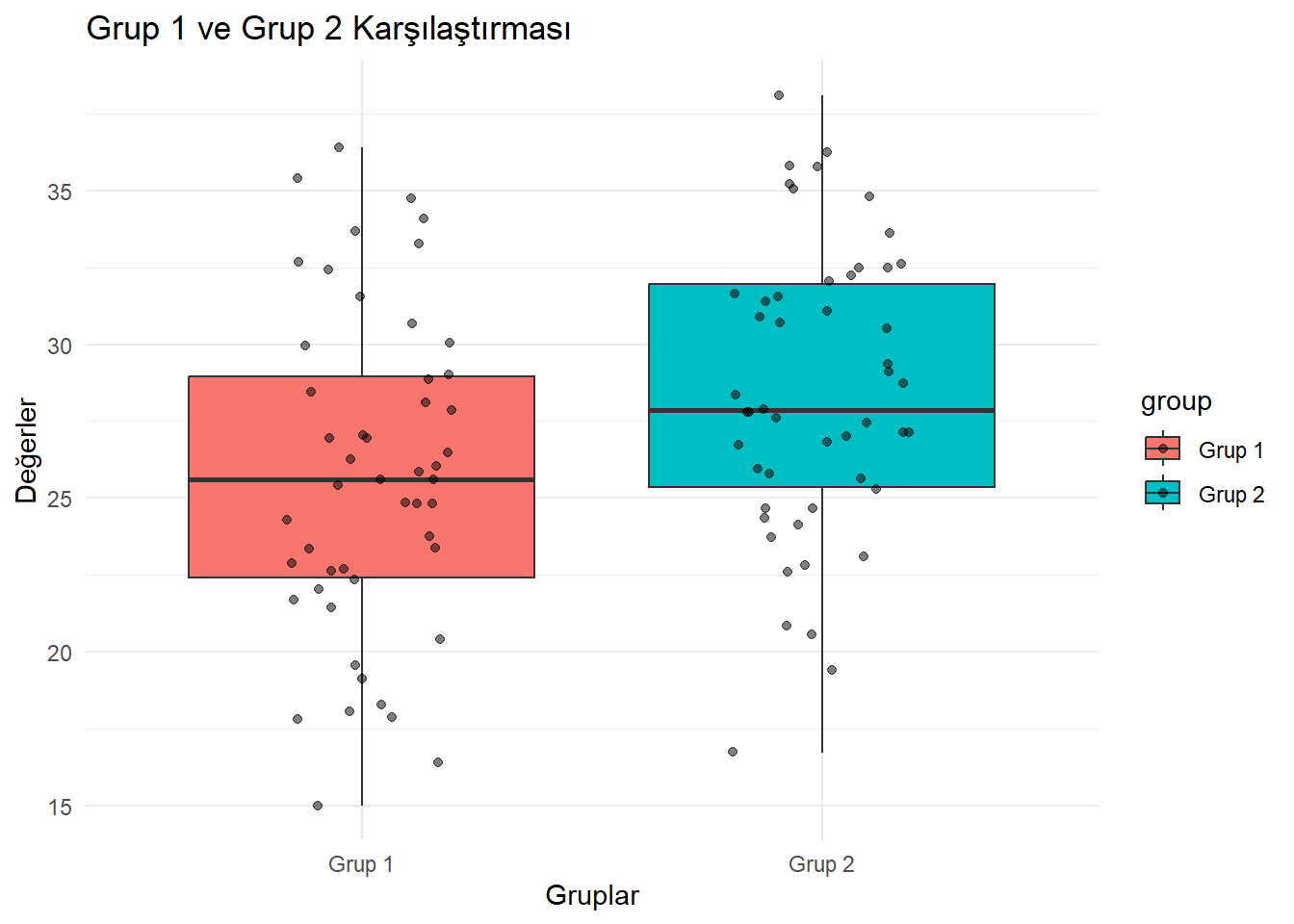

t.test(group1, group2, conf.level = 0.95, alternative = "two.sided")

    Welch Two Sample t-test

data:  group1 and group2
t = -2.7148, df = 96.986, p-value = 0.00785
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -4.7291397 -0.7346981
sample estimates:
mean of x mean of y 
 25.73691  28.46883

Daha iyi bir çıktı elde etmek için yine lsr paketini kullanabiliriz. independentSamplesTTest fonksiyonu, veri seti ile çalışır. Sadece bizim örneğimizde cinsiyet olan grup değişkenini belirtmemiz gerekir. Yapmamız gereken tek şey grup değişkeninin bir faktör olduğundan emin olmaktır.

veri1 <- data.frame ( group = c(rep(1,50),rep(2,50)) , deger = c(group1,group2 ))
veri1$group <- as.factor(veri1$group)

independentSamplesTTest(formula = deger ~ group, 
                        conf.level = 0.95,
                        one.sided = FALSE, 
                        data = veri1)

   Welch's independent samples t-test 

Outcome variable:   deger 
Grouping variable:  group 

Descriptive statistics: 
                 1      2
   mean     25.737 28.469
   std dev.  5.283  4.767

Hypotheses: 
   null:        population means equal for both groups
   alternative: different population means in each group

Test results: 
   t-statistic:  -2.715 
   degrees of freedom:  96.986 
   p-value:  0.008 

Other information: 
   two-sided 95% confidence interval:  [-4.729, -0.735] 
   estimated effect size (Cohen's d):  0.543

α=.05 anlamlılık seviyesi ile grup1 ve grup2 için ortalama puanının popülasyonda aynı olduğu yokluk hipotezini reddediyoruz,\(t_{(96)}=-2.715 ,p<.05 ,CI95=[-4.729, -0.735]\).

Analizleri raporlayacağımız bir diğer paket ise report

library("report")

# Run an independent-samples t test and create a report
report(t.test(group1,group2, conf.level = 0.95, alternative = "two.sided"))
Effect sizes were labelled following Cohen's (1988) recommendations.

The Welch Two Sample t-test testing the difference between group1 and group2
(mean of x = 25.74, mean of y = 28.47) suggests that the effect is negative,
statistically significant, and medium (difference = -2.73, 95% CI [-4.73,
-0.73], t(96.99) = -2.71, p = 0.008; Cohen's d = -0.54, 95% CI [-0.94, -0.14])

Bağımlı örneklem t-testi

Eşleştirilmiş iki veri setimiz olduğunu varsayalım: \(X_1\) ve \(X_2\) . Bu veriler arasındaki fark, \(D = X_1 - X_2 ~ N(\mu_D,\sigma)\) şeklinde tanımlanır.

Amacımız, iki popülasyon ortalamasının \(\mu_1\) ve \(\mu_2\) aynı olup olmadığını test etmektir. Bu, tek bir popülasyonun iki zaman noktasındaki ölçümlerini de temsil edebilir.

Sıfır hipotezi: \(H_0: \mu_D = 0\) (iki popülasyon ortalaması eşittir)

Alternatif hipotez: \(H_1: \mu_D \neq 0\) ((iki popülasyon ortalaması farklıdır)

Anlamlılık düzeyi: \(\alpha\)

Test istatistiği şu şekilde hesaplanır:

\(t = \frac{\bar{D}}{s_D / \sqrt{n}}\)

Burada serbestlik derecesi df şu şekilde hesaplanır:

\(df = n - 1\)

  • \(D\): İki popülasyon (veya iki zaman noktası) arasındaki fark

  • \(\bar{D}\): Farkların örneklem ortalaması

  • \(s_D\): Farkların örneklem standart sapması

  • \(n\): Örneklem büyüklüğü

  • Eğer \(t > t_{\text{kritik}}\) \(\alpha\) anlamlılık düzeyinde, sıfır hipotezini reddederiz.

  • Aksi takdirde, sıfır hipotezini reddetmeyiz.

Bağımlı örneklem t-testi uygulama

Bağımlı örneklem t-testi, aynı bireylerin iki farklı durumda ölçülen değerlerini karşılaştırır.

Örnek veri oluşturma

set.seed(789)
before <- rnorm(30, mean = 70, sd = 10) 
after <- before + rnorm(30, mean = 5, sd = 5)

t-testi uygulama

paired_t_test <- t.test(before, after, paired = TRUE)

Sonuçları gösterme

paired_t_test

    Paired t-test

data:  before and after
t = -5.5709, df = 29, p-value = 5.199e-06
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -7.505526 -3.474479
sample estimates:
mean difference 
      -5.490002 
paired_data <- data.frame( time = rep(c("Önce", "Sonra"), 
                            each = 30), 
                           value = c(before, after), 
                           subject = rep(1:30, 2) )

ggplot(paired_data, aes(x = time, y = value, group = subject)) + 
  geom_line(alpha = 0.3) + 
  geom_point(aes(color = time), size = 3) + 
  theme_minimal() + 
  labs(title = "Önce ve Sonra Ölçümleri",
       x = "Zaman", y = "Değerler")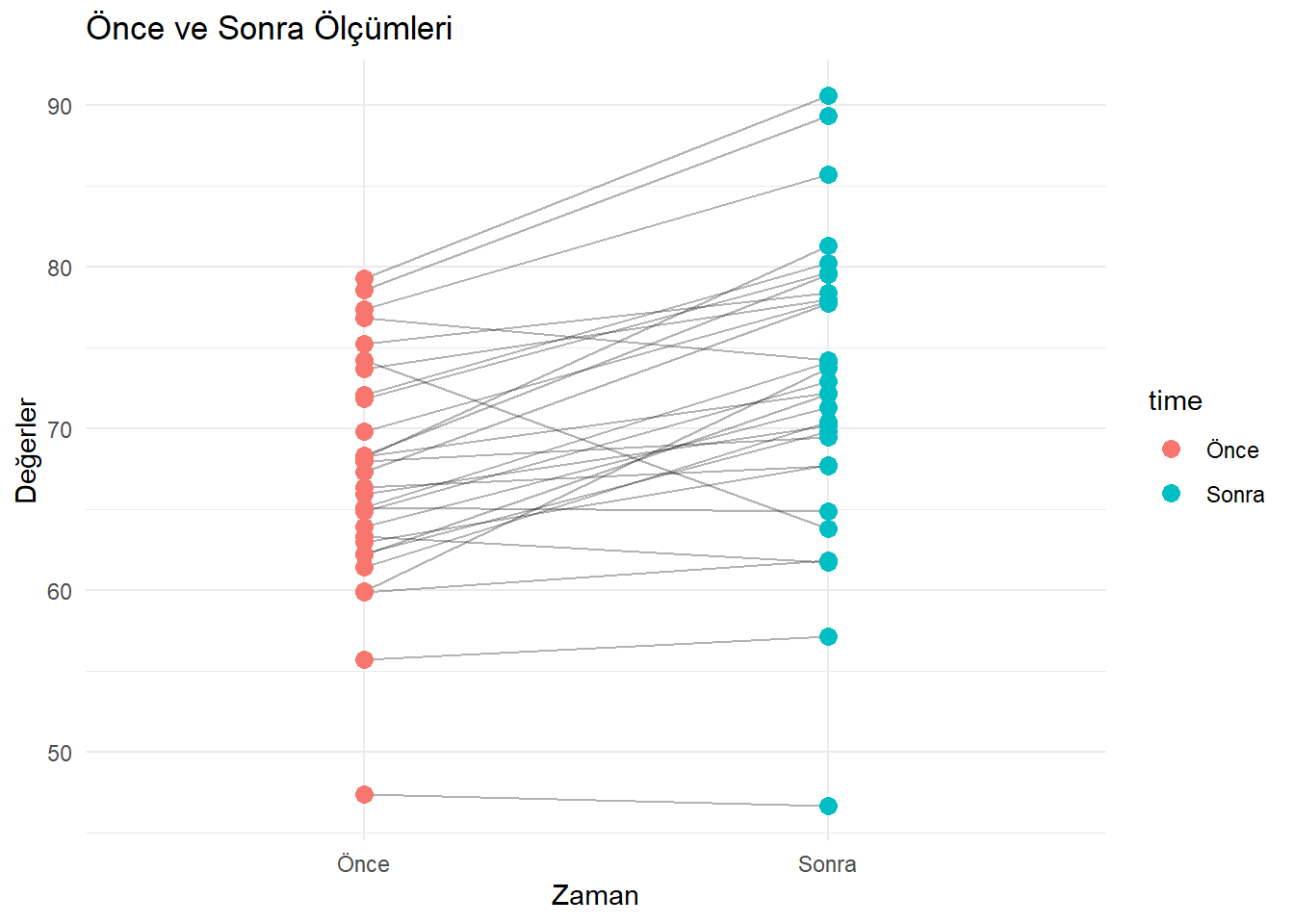

lsr paketi ile sonuc alalım

pairedSamplesTTest(formula = ~ before + after,
                   conf.level = 0.95,
                   one.sided = FALSE)

   Paired samples t-test 

Variables:  before , after 

Descriptive statistics: 
            before  after difference
   mean     67.191 72.681     -5.490
   std dev.  7.087  9.258      5.398

Hypotheses: 
   null:        population means equal for both measurements
   alternative: different population means for each measurement

Test results: 
   t-statistic:  -5.571 
   degrees of freedom:  29 
   p-value:  <.001 

Other information: 
   two-sided 95% confidence interval:  [-7.506, -3.474] 
   estimated effect size (Cohen's d):  1.017

α=.05 anlamlılık seviyesi ile önce ve sonra puanlarının evrende aynı olduğu yokluk hipotezini reddediyoruz,\(t_{(29)}=-4.285 ,p<.05 ,CI95=[-5.954, -2.107]\) .

Non-parametrik Testler

T-testlerinin varsayımları karşılanmadığında (örneğin, normallik varsayımı), non-parametrik testler kullanılır. T-testlerinin non-parametrik karşılıkları şunlardır:

  1. Tek örneklem t-testi → Wilcoxon işaretli sıra testi
  2. Bağımsız örneklem t-testi → Mann-Whitney U testi
  3. Bağımlı örneklem→ Wilcoxon işaretli sıra testi

Wilcoxon İşaretli Sıra Testi

Örnek veri oluşturma

set.seed(101) 
data_np <- rexp(50, rate = 0.5)

Wilcoxon işaretli sıra testi

wilcox_test <- wilcox.test(data_np, mu = 2)

Sonuçları gösterme

wilcox_test

    Wilcoxon signed rank test with continuity correction

data:  data_np
V = 357, p-value = 0.006873
alternative hypothesis: true location is not equal to 2

Mann-Whitney U Testi

Örnek veri oluşturma

set.seed(102) 
group1_np <- rexp(40, rate = 0.5) 
group2_np <- rexp(40, rate = 0.7)

Mann-Whitney U Testi

mw_test <- wilcox.test(group1_np, group2_np)

Sonuçları gösterme

mw_test

    Wilcoxon rank sum exact test

data:  group1_np and group2_np
W = 948, p-value = 0.1566
alternative hypothesis: true location shift is not equal to 0
np_data_long <- data.frame( value = c(group1_np, group2_np), 
                    group = rep(c("Grup 1", "Grup 2"), 
                                each = 40) )

ggplot(np_data_long, aes(x = group, y = value, 
                         fill = group)) + 
  geom_boxplot(trim = FALSE) + 
  geom_boxplot(width = 0.1, fill = "white") + 
  theme_minimal() + 
  labs(title = "Grup 1 ve Grup 2 Karşılaştırması
       (Non-parametrik)", x = "Gruplar", y = "Değerler")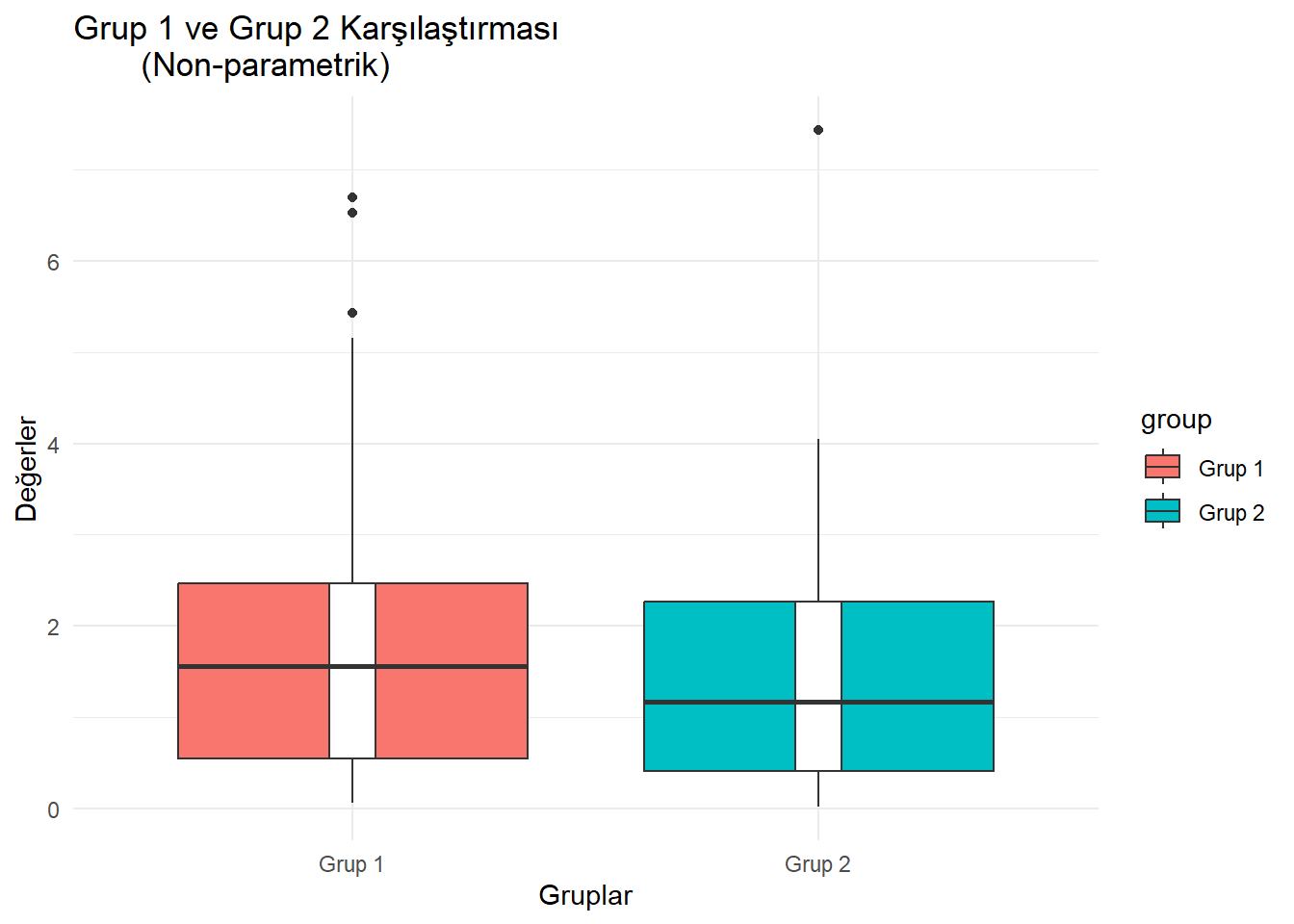

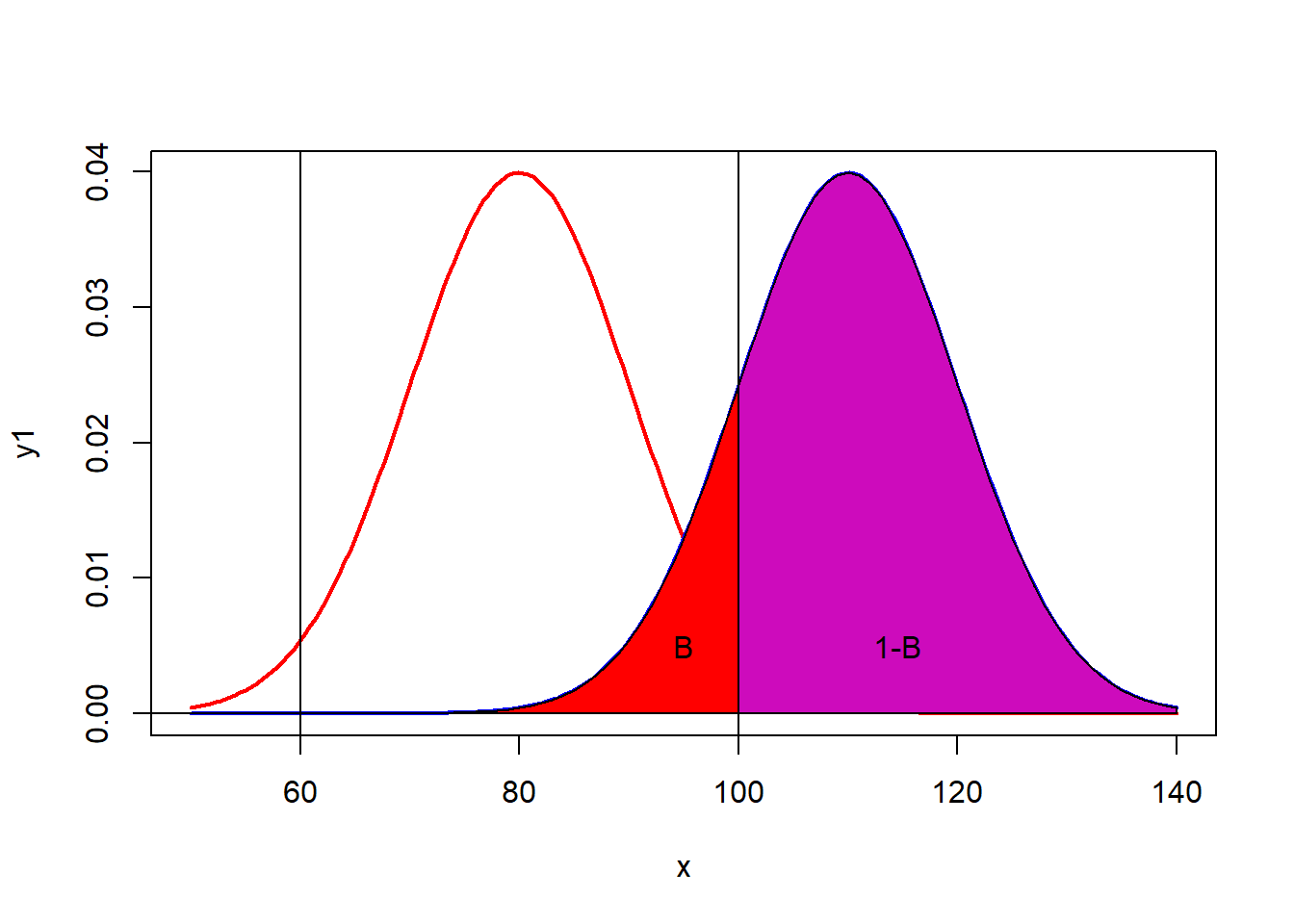
Görselleştirme

Kırmızı dağılım, \(H_0\) hipotezi doğru olduğunda örneklem ortalamalarının dağılımını ifade eder. Mavi dağılım ise \(H_0\) hipotezi doğru olmadığında örneklem ortalamalarının dağılımıdır. Şimdi,\(H_0\) nin doğru olduğu durumda, evrenden çok sayıda örneklem seçtiğimizi düşünelim.

Ortalamaları 80 olan bir evrenden seçilen örneklemleri ele alalım. Seçilen bir örneklem ortalaması 80’e yakın bir değer olabilir, 90 olabilir, hatta nadir de olsa 120 veya 130 gibi bir değere de ulaşabilir. Kırmızı dağılımda, 95. yüzdelik dilime dikey bir çizgi çekelim. Bu çizgi, tek yönlü t testi için sınır değeri temsil eder. Eğer bu çizginin sağında bir değer elde edilirse, \(H_0\) reddedilir. Ancak, seçilen örneklemlerin %5’inde, şans eseri bu sınır değerden daha büyük bir değer elde edilebilir. Bu durum, aynı zamanda I. tip hata olarak adlandırılır.

I. tip hata, doğru olan \(H_0\) hipotezini reddetmek anlamına gelir.

  • Doğru olan \(H_0\) hipotezini reddetme
# TEK KUYRUK TEST
x<-seq(50,140,length=200)
y1<-dnorm(x,80, 10)
plot(x,y1,type='l',lwd=2,col='red')
y2<-dnorm(x,110, 10)
lines(x,y2,type='l',lwd=2,col='blue')
abline(v=qnorm(0.95,80,10))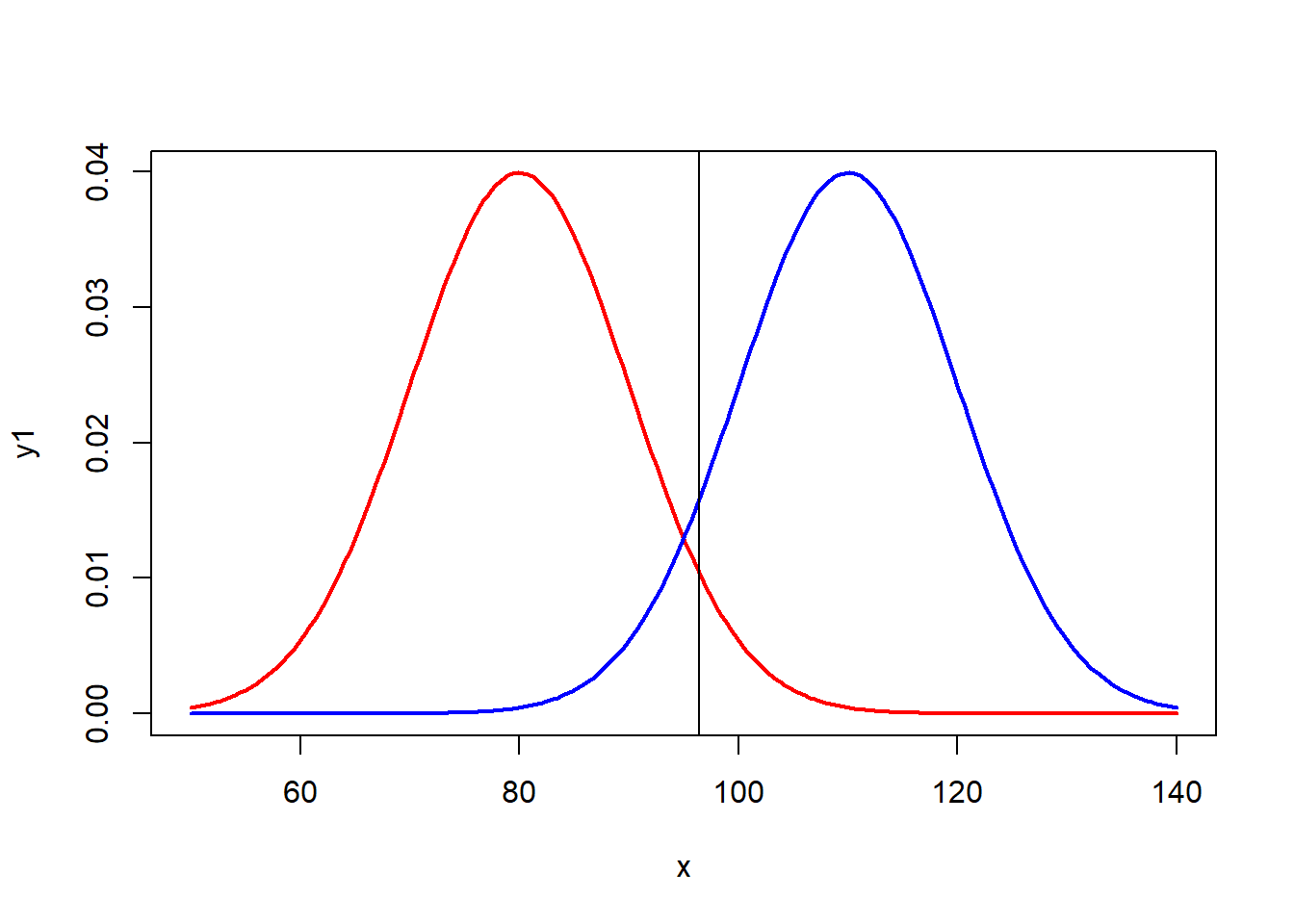

Eğer testi yönsüz yapacak olursak, %2.5 ve %97.5 yüzdeliklerine çekilen çizgiler kritik bölgenin alanını belirleyecektir. Yani, seçilen örneklemlerin %5’i 60’tan küçük veya 100’den büyük bölgeye düşerse, \(H_0\) reddedilecektir. Bu bölge aynı zamanda I. tip hata bölgesidir.

x=seq(50,140,length=200)
y1=dnorm(x,80, 10)
plot(x,y1,type='l',lwd=2,col='red')
y2=dnorm(x,110, 10)
lines(x,y2,type='l',lwd=2,col='blue')
abline(v=qnorm(0.025,80,10))
abline(v=qnorm(0.975,80,10))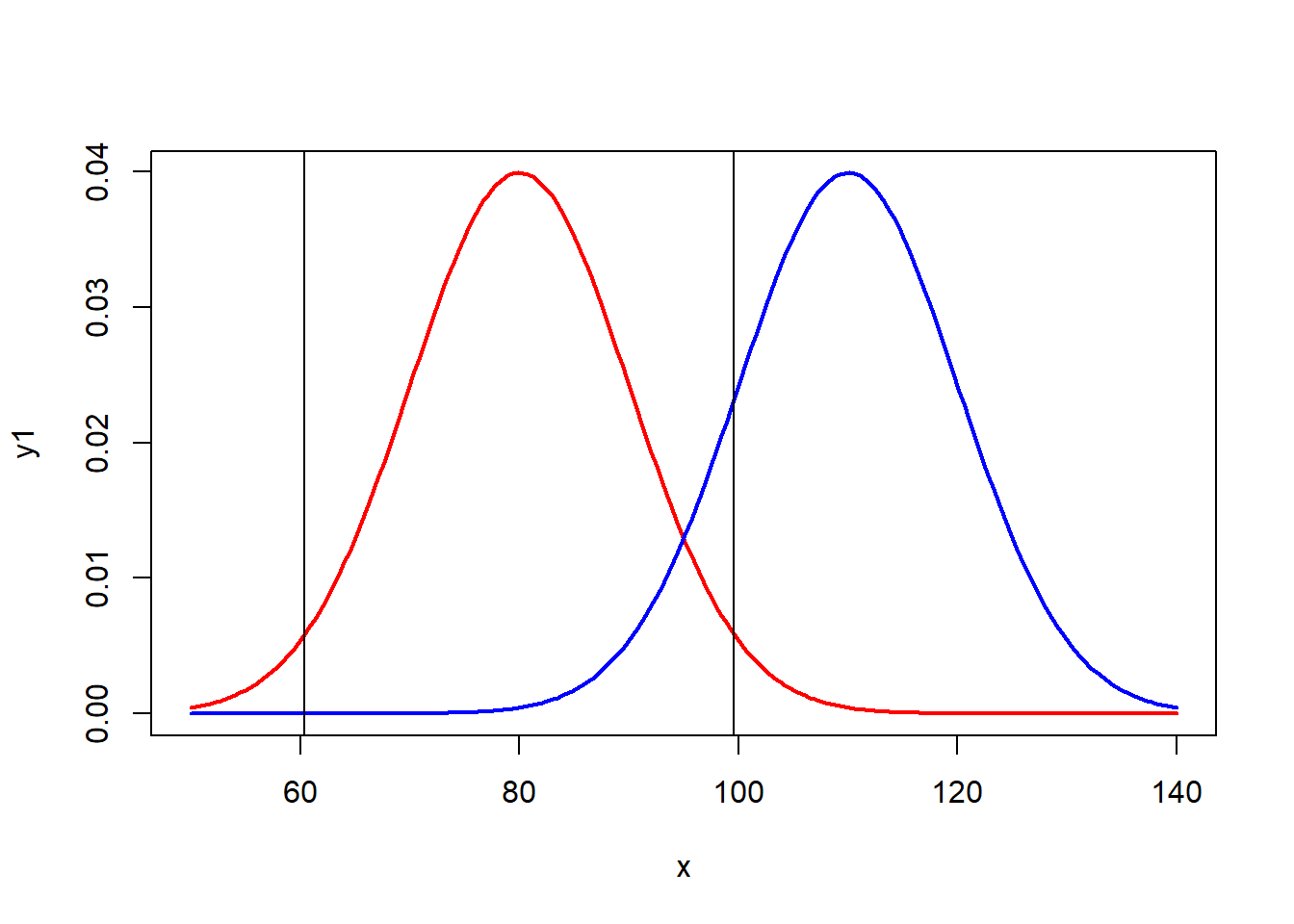

Alfa bölgesini tarama: Eğer p-değeri, alfa değerine eşit ya da daha küçükse, \(H_0\) reddedilir.

x=seq(50,140,length=200)
y1=dnorm(x,80, 10)
plot(x,y1,type='l',lwd=2,col='red')
y2=dnorm(x,110, 10)
lines(x,y2,type='l',lwd=2,col='blue')
cord.x1 <- c((round(qnorm(0.975, 80, 10))),seq((round(qnorm(0.975, 80, 10))), 120,1),120) 
cord.y1 <- c(0,dnorm(seq((round(qnorm(0.975, 80, 10))), 120, 1), 80, 10),0) 
polygon(cord.x1,cord.y1,col='red')
cord.x2 <- c(50,seq(50,round(qnorm(0.025, 80, 10),1)),round(qnorm(0.025, 80, 10))) 
cord.y2 <- c(0,dnorm(seq(50,round(qnorm(0.025, 80, 10),1)), 80, 10),0) 
polygon(cord.x2,cord.y2,col='red')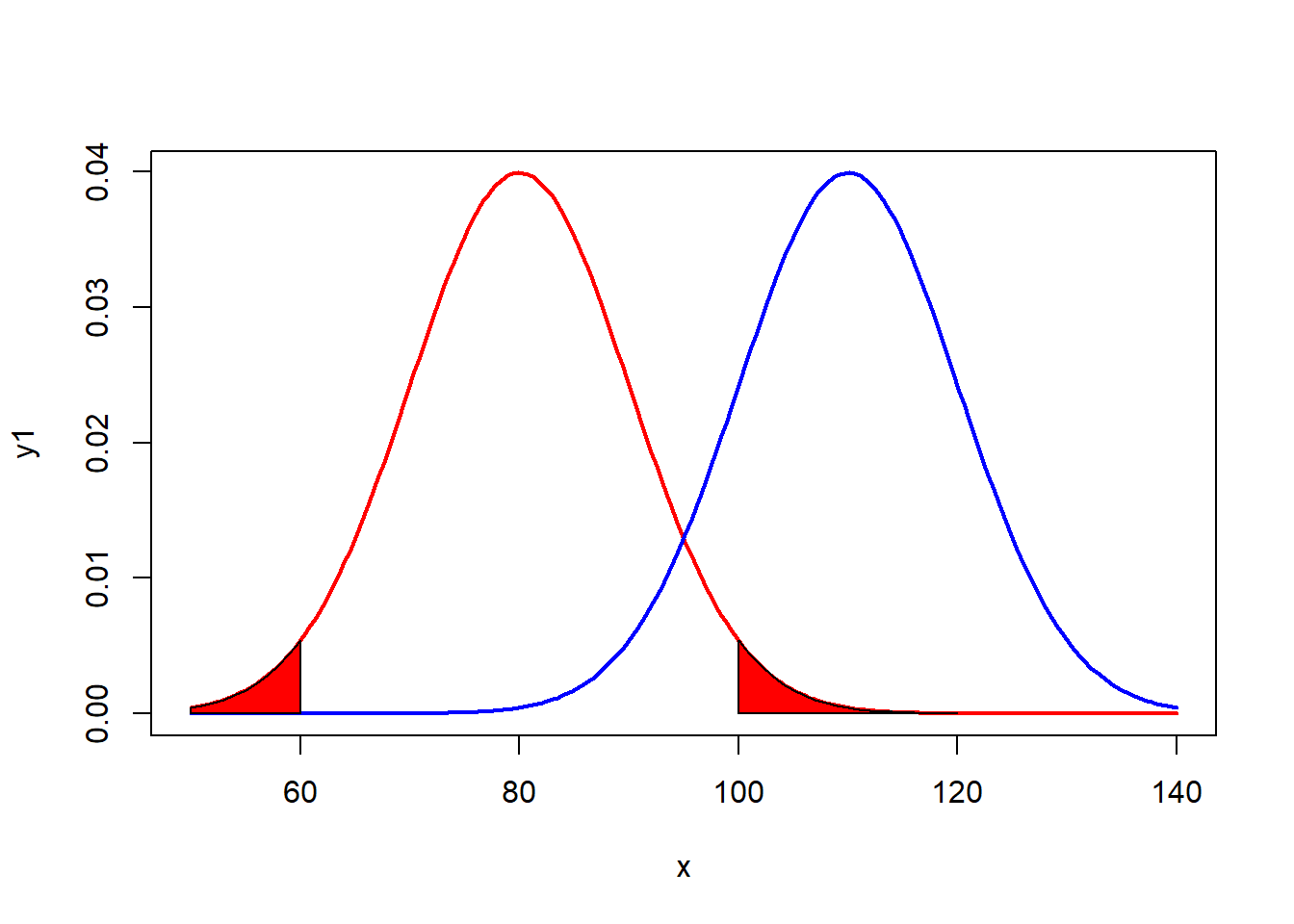

Mavi dağılım doğru ise ve seçilen yüksek ortalamalar ile \(H_0\) hipotezi rededilir.

Alternatif hipotez doğru ise yanlış olan \(H_0\) hiptezini red edememe durumu

    1. tip hata (beta)
x=seq(50,140,length=200)
y1=dnorm(x,80, 10)
plot(x,y1,type='l',lwd=2,col='red')
y2=dnorm(x,110, 10)
lines(x,y2,type='l',lwd=2,col='blue')
cord.x2<- c(0,seq((round(1-qnorm(0.025,110,10))),100,1),100)
cord.y2 <- c(0,dnorm(seq((round(1-qnorm(0.025, 110, 10))), 100, 1), 110, 10),0) 
polygon(cord.x2,cord.y2,col='red')
abline(v=round(qnorm(0.975, 80, 10, lower.tail=T)))
abline(v=round(qnorm(0.025, 80, 10, lower.tail=T)))
text(95,0.005, "? ",xpd=5)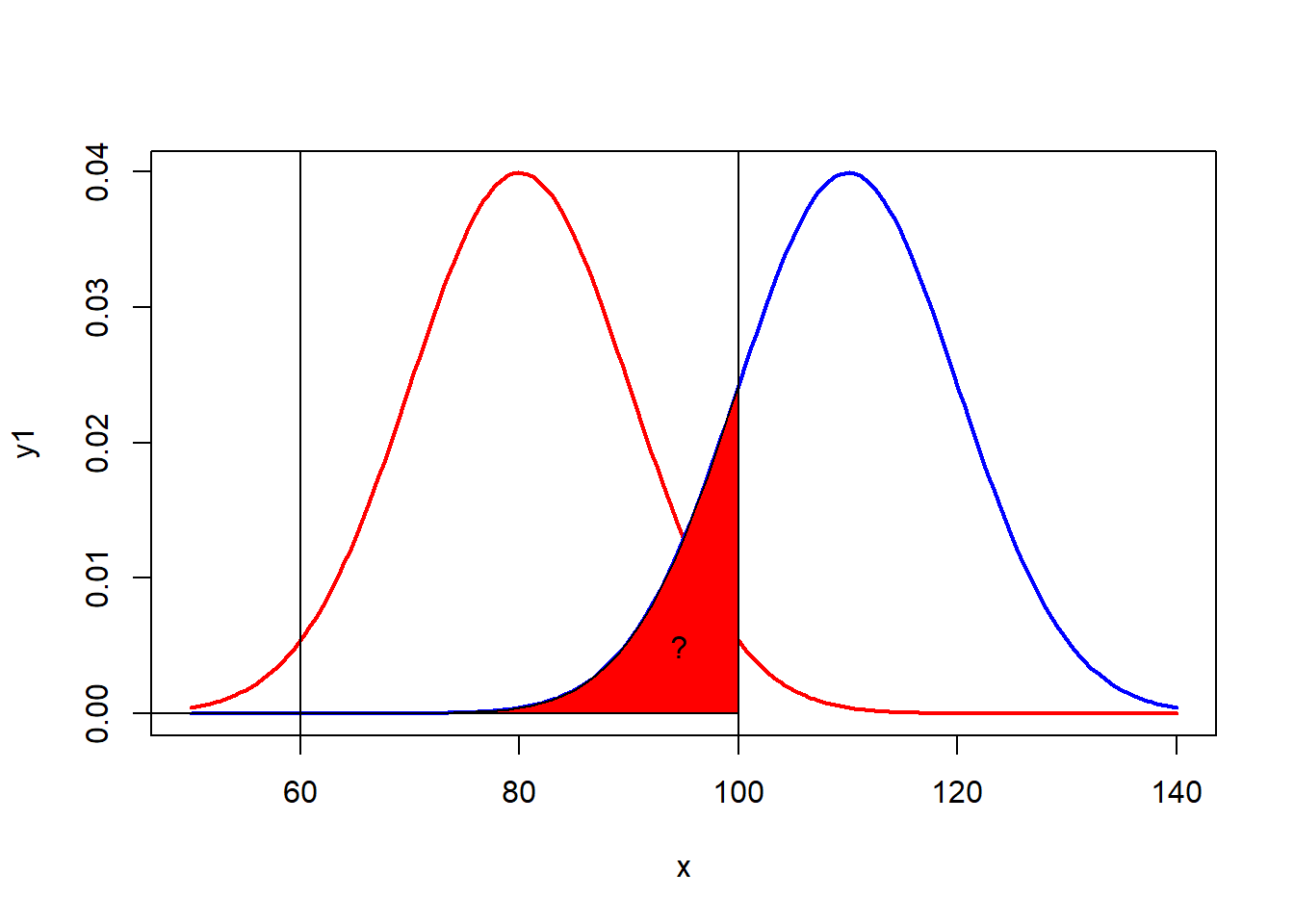

# Istatistiksel guc ise  1-beta, 
# yanlis olan Ho'i reddetme
x<- seq(50,140,length=200)
y1<- dnorm(x,80, 10)
plot(x,y1,type='l',lwd=2,col='red')
y2<- dnorm(x,110, 10)
lines(x,y2,type='l',lwd=2,col='blue')
cord.x2<- c(0,seq((round(1-qnorm(0.025,110,10))),100,1),100)
cord.y2 <- c(0,dnorm(seq((round(1-qnorm(0.025, 110, 10))), 100, 1), 110, 10),0) 
polygon(cord.x2,cord.y2,col='red')
abline(v=round(qnorm(0.975, 80, 10, lower.tail=T)))
abline(v=round(qnorm(0.025, 80, 10, lower.tail=T)))
cord.x1 <- c(100,seq(round(qnorm(0.975, 80, 10, lower.tail=T)), 140,1),140) 
cord.y1 <- c(0,dnorm(seq(round(qnorm(0.975, 80, 10, lower.tail=T)),140, 1), 110, 10),0) 
polygon(cord.x1,cord.y1,col='6')
text(95,0.005, "B",xpd=5)
text(115,0.005, "1-B ",xpd=5)