Regresyon Modelleri

paketler

library(haven)
library(dplyr)
library(knitr) # 
library(ggplot2)
library(QuantPsyc) #lm.beta fonksiyonu için standartlaştırılmış regresyon katsayısı
library(psych) #describe fonksiyonu ile betimsel istatistik hesapladık
library(broom) # model sonuçlarını derli toplu hale getirmek için
library(outliers) # standart puan hesaplamak için
 library(car) # regresyon grafiklerini çizdirmek için (avPlots)
 library(ggfortify) # regresyon artık grafiklerini çizdirmek icin (autoplot)
library(lavaan) # yapısal eşitlik modellemesi olarak regresyon
library(lavaanPlot) # lavaan model grafik çizimi

library(semptools) # regresyon ve yapısal eşitlik modelleme için yardımcı fonksiyonlar özellikle anlamlılık düzeyi
library(semPlot) # lavaan model grafik çizimi
library(olsrr) # regresyon model tanı testleri için etkili gözlem gibi

library(fastDummies) # kategorik değişkenlerden dummy değişken oluşturmak için
library(interactions)

Bilindiği üzere, t-testi, varyans analizi gibi ortalama farkları ile ilgili hipotez testleri değişkenler arasındaki ilişkiye dair herhangi bir bilgi vermemektedir.
Oysa serpilme diyagramlarına bakıldığında değişkenler arasında bir ilişki olabileceği hissedilebilmekte fakat bu tür analizlerle bu ilişkiler ortaya koyulamamaktadır.
Dolayısıyla değişkenler arasındaki ilişkinin şeklini, yönünü ve kuvvetini belirleyebilmemiz için yeni metotlara ihtiyaç vardır. Bu metotlar ise genel olarak regresyon (eğri uydurma) ve korelasyon analizi olarak adlandırılır.

1 Regresyon Kullanım Alanları

Tarımda belli ürünlerin verimi etkileyen toprak türü, tohum, sulama v.b. faktörlerin saptanması ve bunlar yardımıyla belli şartlarda alınacak ürün miktarının kestirilmesi tarımın önemli konusudur.
Bir değişkenin değerlerinin ilgili başka değişkenler yardımıyla kestirilmesi, günlük yaşamımızın, ticaretin ekonominin, doğa ve sosyal bilimlerin önemli konularını içendedir.
günlük yaşamımızın, ticaretin ekonominin, doğa ve sosyal bilimlerin pek çok alanındaki çalışmalarda iki ya da daha çok değişken arasında fonksiyonel ilişkiler vardır. Bu ilişkiler matematiksel bir denklem yazılabilir.

Örneğin taksi hizmeti ödenen $ücret = a + bx$
a: sabit (taksimetre açılış ücreti)
b: her kilometrede artan ücret

2 Regresyon Kullanım Alanları

Regresyon çözümlemenin temel amacı; bağımlı değişken ile bağımsız değişken(ler) arasındaki ilişkiyi matematiksel modelle açıklayarak bağlantılar bulmak ve bağımsız değişken(ler) yardımıyla bağımlı değişkenli kestirmek şeklinde özetlenebilir.
Sosyal bilimlerde değişkenler arasındaki ilişkiler bir dereceye kadar fonksiyoneldir. (taksimetre örneği kadar net değildir!) Bu ilişkiye probabilisitik ilişki denir.
Sosyal bilimlerde değişkenler arasındaki ilişkilerin matematiksel olarak kesin ifadelerle yazılamaması, bu değişkenlere ait önceki bilgiler yardımıyla elde edilmesi ve matematiksel ifadelerin bu bilgilere dayanılarak yazılması yolunu açmıştır.
Regresyon terimi 19. yüzyılda İngiliz istatistikçisi Francis Galton tarafından bir biyolojik inceleme için ortaya atılmıştır. Bu incelemenin ana konusu kalıtım olup, aile içinde baba ve annenin boyu ile çocukların boyu arasındaki bağlantıyı araştırmakta ve çocukların boylarının bir nesil içinde eski ata nesillerinin ortalamasına geri döndüklerini yani bir nesil içinde ortalamaya geri dönüş olduğu inceleme konusudur.

3 Basit Doğrusal Regresyon

Bir bağımsız $X$ değişkeninin değerlerinden ona bağlı değişkeninin değerlerinin kestirilmesini sağlayan denkleme $Y$’in $X$’e göre regresyonu denir.

\[Y= bx + a\] - Regresyon denkleminde $b$ doğrunun eğimidir – $X$’in 1 puanlık değişimine karşılık Y’nin ne kadar değişeceğini belirtir. (buna regresyon katsayısı denir)

$a$ ise $Y$-kesişim noktasıdır – $X$ sıfıra eşit olduğunda $Y$’nin alacağı değerdir (buna regresyon sabiti denir)
Lise matematik puanlarından yararlanarak üniversite genel matematik puanlarını kestirme amacıyla üniversite genel matematik dersini alan öğrencilerden uygun bir örneklem alınmıştır.

lise_not <- c(18,35,53,24,64,58,32,39,64,82,32,49,48,70,57)
uni_not  <- c(33,46,47,21,73,55,74,32,56,68,43,46,68,84,61)
veri <- data.frame(lise_not, uni_not)

Regresyon analizi yapmadan önce saçılım diagramı incelenmelidir. Puanlar saçılım grafiğinde tek bir doğru oluşturmamaktadır. Ancak doğru oluşturma eğilimleri vardır.

ggplot2::ggplot(veri, aes(x = lise_not, y = uni_not)) + 
  geom_point() +   
  geom_smooth(method = "lm", se = F)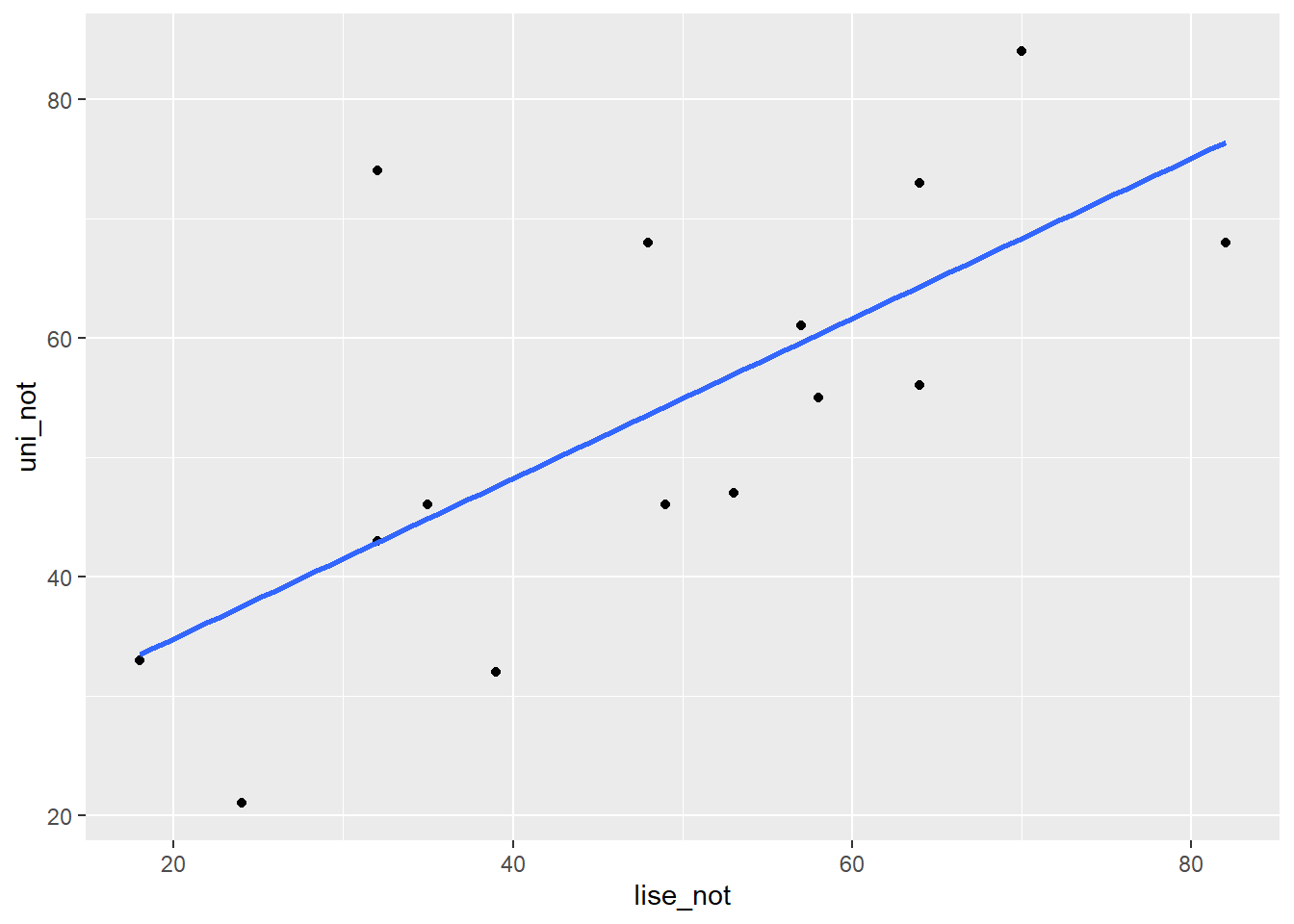

Noktalardan olabildiğince yakın geçecek bir doğru çizilebilirse bu doğrudan yararlanarak $X$ puanı bilinen öğrencilerin $Y$ puanları kestirilebilir.

basitreg <- lm(uni_not ~ lise_not , veri)
summary(basitreg)


Call:
lm(formula = uni_not ~ lise_not, data = veri)

Residuals:
     Min       1Q   Median       3Q      Max 
-16.4748  -8.3488  -0.4494   5.0374  31.1580 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  21.3733    10.1955   2.096   0.0562 . 
lise_not      0.6709     0.1983   3.383   0.0049 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 13.45 on 13 degrees of freedom
Multiple R-squared:  0.4681,    Adjusted R-squared:  0.4272 
F-statistic: 11.44 on 1 and 13 DF,  p-value: 0.004904

4 En küçük kareler yöntemi

Bu yönteme göre a ve b öyle bir belirlenmelidir ki dağılımdaki noktaların, doğrunun etrafındaki değişkenliği en aza indirgenmiş olmalıdır.
Regresyon doğrusu, noktalar ile regresyon doğrusu arasındaki sapmaların kareler toplamı en az olacak şekilde, saçılım grafiğindeki noktalar kümesine en uygun yere çizildiğinden bu ölçüte en küçük kareler ölçütü adı verilir.

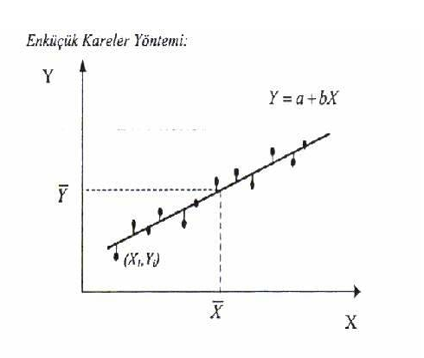
$Y$ değeri ve regresyon doğrusundaki $Y′$ arasındaki farkın en küçük olacak şekilde yerleştirilir.
$\sum(Y-Y′)^2$ en küçük olacak şekilde yerleştirir.
$b_{yx}=\frac{n\sum{XY}-\sum{X}\sum{Y}}{n\sum{X^2}-(\sum{X})^2}$
$a_{yx}=\frac{n\sum{Y}-b_{YX}\sum{X}}{n}$
$b_{yx}$ hesaplama
$b_{YX}=\frac{n\sum{XY}-\sum{X}\sum{Y}}{n\sum{X^2}-(\sum{X})^2}$

n <- length(lise_not)
byx = (n*sum(lise_not*uni_not)-sum(lise_not)*sum(uni_not))/
  (n*sum(lise_not^2) - sum(lise_not)^2)
byx

[1] 0.670898

Regresyon doğrusunun eğimi, değişkenlerin standart sapmalarının oranlarıyla bunlar arasındaki korelasyonun çarpımına eşittir.

(sd(uni_not)/sd(lise_not))*cor(lise_not,uni_not)

[1] 0.670898

$a_{yx}$ hesaplama
$a_{yx}=\frac{n\sum{Y}-b_{yx}\sum{X}}{n}$

attach(veri)
ayx = (sum(uni_not) - byx*sum(lise_not))/15
ayx

[1] 21.37326

5 Kestirimin Standart Hatası

Kestirim sonunda $Y$ değişkeninin gözlenen değerleri ile regresyon değerleri $Y'$ arasında fark olmaması veya bu farkın olabildiği kadar küçük olması istenir.
Gözlenen $Y$ ve kestirilen $Y'$ değerleri arasındaki farklar kestirimdeki hatalardır. Bu farkların karelerinin ortalamasının kare köküne kestirimin standart hatası adı verilir.
\[S_{yx}=\sqrt{\sum{\frac{(Y-Y')^2}{n-2}}}\]
\[S_{yx}=\sqrt{\frac{\sum{Y^2}-a\sum{Y}-b\sum{XY}}{n-2}}\]
Ortak dağılımın için kestirimin standart hatası tek değişkenli dağılımın standart sapmasına benzer.
Standart sapma tek değişkenli dağılımın ortalamadan farkının standart bir ölçüsü olduğu gibi, kestirimin standart hatası da noktaların standart regresyon çizgisinden farkının ölçüsüdür.
Bu nedenle kestirimin standart hatası verilen X değeri için kestirilen Y değerinin standart sapması şeklinde okunabilen $S_{yx}$ sembolü ile gösterilir.

$X$ değerlerinden kestirilen $Y'$ ’lerin standart hatası

sqrt((sum(uni_not^2)-ayx*sum(uni_not)-
       byx*(sum(uni_not*lise_not)))/13)

[1] 13.44511

res <- basitreg$residuals

sqrt(sum((res - mean(res)) ^ 2 / (length(res)-2)))

[1] 13.44511

5.1 Basit Doğrusal Regresyon Uygulama

basitreg <- lm(uni_not ~ lise_not , veri)
library(broom)
glance(basitreg) %>% kable()

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.4681284	0.4272152	13.44511	11.44199	0.0049036	1	-59.19005	124.3801	126.5042	2350.021	13	15

$R$ İki değişken arasında pearson korelasyon katsayısı
$R-Square:$ Determinasyon katsayısı/bağımsız değişkenin bağımlı değişken üzerindeki açıklama oranı
$\text{Adjusted R Square:}$ Düzeltmiş determinasyon katsayısı, şans eseri açıklanan değişimin neden olduğu hatanın arındırılmış hali.
$\text{Standart Kestirimin Hatası:}$ Hata teriminin standart sapmasıdır.
Tablodaki $p$ değeri regresyon modelindeki yordanan ve yordayan değişkenler arasındaki ilişki için hesaplanan değerin anlamlı olup olmadığını göstermektedir.

glance(basitreg)[,c(1,2,4,6,5)]

Yani regresyon modelinde lise matematik puanları ile genel matematik puanları arasında doğrusal ilişki anlamlı düzeydedir. Regresyon modelindeki $\text{df}$ 1 olması nedeni, regresyon modelindeki sabit ve eğimi katsayı olarak almasıdır. 2-1
$p$ değerleri sabitin ve yordayıcı değişkenin katsayısının anlamlılık testi sonuçları

tidy(basitreg)

Çoklu regresyon her bir bağımsız değişkendeki değişikliklerin bağımlı değişkendeki değişikliklerle ne ölçüde ilişkili olduğunu kestirir. Ancak bağımsız değişkenler arasındaki korelasyon yordama sürecini zorlaştırır.

6 Bağımsız değişkenler arasındaki ilişki

ceteris paribus

Örneğin, $X_1$ ve $Y$ arasındaki korelasyon katsayısı 0.40, $X_2$ ve $Y$ arasındaki korelasyon katsayısı 0.60, $X_1$ ve $X_2$ arasındaki korelasyon katsayısı sıfır ise, $Y$’nin varyansının iki değişken tarafından açıklanan toplam oranı iki değişkenin $Y$ ile korelasyonlarının kareleri toplamından elde edilebilir:

$0.40^2 + 0.50^2 = 0.16 + 0.25 = 0.41$

Ancak, uygulamada çoğunlukla $X_1$ ve $X_2$ birlikte değişim gösterirler ve iki değişkenin $Y$ ile korelasyonlarının kareleri toplamı çok yüksek bir oran verir.
Bunun nedeni, iki bağımsız değişkenin aralarındaki korelasyondan dolayı her bir bağımsız değişken tarafından açıklanan $Y$ varyansının bir kısmının üst üste gelmesidir.

Modeldeki bağımsız değişkenler arasındaki ilişkilerin kontrol altına alınması, modeldeki bir değişkenin bağımlı değişken üzerindeki etkisini incelerken, modeldeki diğer bütün değişkenlerin sabit tutulmasıdır (ceteris paribus)
1. Neden sabit tutmaya ihtiyaç var: “Pizza ve Kilo Örneği” “Daha fazla pizza yemek kilo aldırır mı?”

Senaryo A: Ahmet her gün 3 pizza yiyor ama aynı zamanda günde 20 km koşuyor. Kilo verir.

Senaryo B: Ayşe her gün 3 pizza yiyor ve hiç hareket etmiyor. Kilo alır.

Eğer sadece pizzaya bakarsak kafamız karışabilir. “Pizza yemek kilo verdirir” diyebilir miyiz (Ahmet örneğindeki gibi)? Hayır.

Ceteris Paribus’un Tanımı: Pizzanın kilo üzerindeki gerçek etkisini ölçmek istiyorsak, Ahmet’in koşusunu, genetiğini, uyku düzenini ve diğer her şeyi dondurmamız/sabitlememiz gerekir.

Yani; “Diğer tüm koşullar (spor, metabolizma, uyku) sabit kalmak şartıyla, daha fazla pizza yemek kilo aldırır.” İşte bu cümledeki “sabit kalmak şartıyla” kısmı, Ceteris Paribustur.

7 Uygulama

veri seti 🔗 Performans.sav
Performans: Öğrencilerin matematik performans düzeyleri olup eşit aralık ölçeğinde ölçülen sürekli bir değişkendir.
Motivasyon: Öğrencilerin motivasyon düzeyleri olup eşit aralık ölçeğinde ölçülen sürekli bir değişkendir.
Kaygı: Öğrencilerin kaygı düzeyleri olup eşit aralık ölçeğinde ölçülen sürekli bir değişkendir.
Güven: Öğrencilerin matematiğe karşı güven düzeyleri olup eşit aralık ölçeğinde ölçülen sürekli bir değişkendir.
Analize başlamadan önce değişkenlerin betimsel istatistikleri ve değişkenler arası korelasyonlar incelenmelidir.

Betimsel İstatistikler

performans <- read_sav("data/Performans.sav")
psych::describe(performans) %>% kable(digit=3)

	vars	n	mean	sd	median	trimmed	mad	min	max	range	skew	kurtosis	se
Performans	1	15	18.176	7.828	18.041	17.925	9.215	4.112	35.501	31.390	0.283	-0.384	2.021
Motivasyon	2	15	39.933	10.025	40.000	40.154	10.378	22.000	55.000	33.000	-0.178	-1.173	2.588
Kaygi	3	15	18.071	4.769	18.298	17.860	2.247	10.720	28.169	17.449	0.593	-0.079	1.231
Guven	4	15	21.630	7.375	22.000	21.308	5.708	8.750	38.700	29.950	0.300	-0.101	1.904

Korelasyon değerleri ve anlamlılığı

library(broom)
cor_1 <- cor.test(~ Performans + Motivasyon , data = performans)
tidy(cor_1)  %>% kable(digit=3)

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.824	5.252	0	13	0.54	0.94	Pearson’s product-moment correlation	two.sided

cor_2 <- cor.test(~ Performans + Kaygi , data = performans)
tidy(cor_2)[,c(1,3)]  %>% kable(digit=3)

estimate	p.value
-0.241	0.388

cor_3 <- cor.test(~ Motivasyon + Kaygi , data = performans)
tidy(cor_3)[,c(1,3)] %>% kable(digit=3)

estimate	p.value
0.147	0.601

İlişki Grafiği

library(GGally)
ggpairs(performans[,1:3])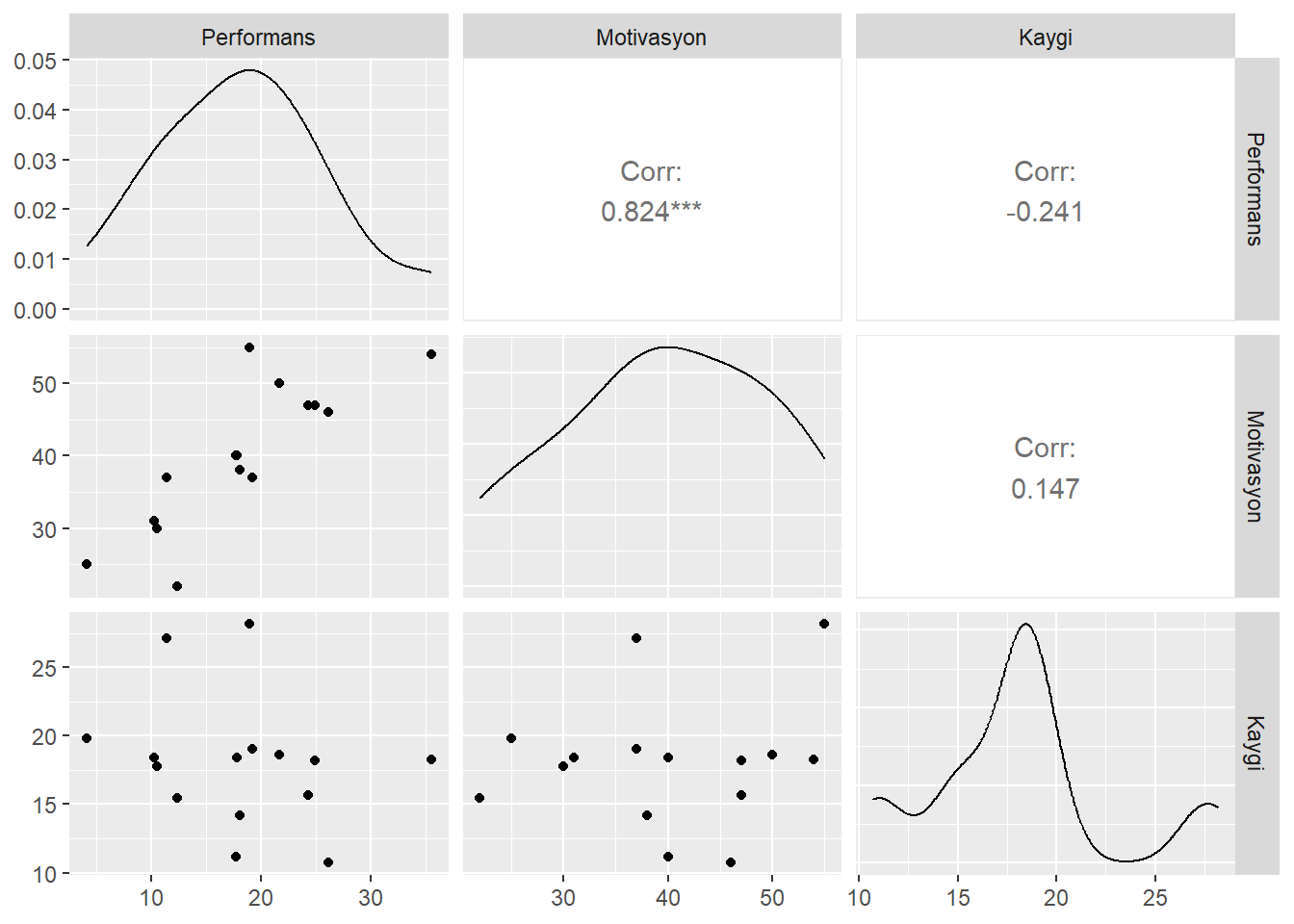

3D grafik

library(scatterplot3d)
scatterplot3d(performans[,1:3],
              pch = 16,
              color="steelblue", 
              angle=75)

3D grafik

scatterplot3d(performans[,1:3],
              pch = 16, color="steelblue",
              angle=75,
              box = FALSE,type = "h")

3D grafik

library(rgl)
plot3d(performans$Performans, performans$Motivasyon, performans$Kaygi,
xlab = "Performans", ylab = "Motivasyon", 
zlab = "Kaygi", 
type = "s",size = 1.5,col = "red")
rglwidget()

8 Çoklu korelasyon katsayısı

$R^2$ değeri çoklu korelasyon katsayısı (multiple correlation coefficient) olup bağımlı değişkenin gözlenen değerleri ile bağımsız değişkenlerin en iyi doğrusal kombinasyonu arasındaki korelasyondur.
En iyi doğrusal kombinasyon, bağımlı değişkenin bağımsız değişkenlerden yordanmasında, daha iyi bir iş yapacak regresyon katsayıları kümesi olmadığı anlamına gelir.

model <- lm(Performans ~ Motivasyon + Kaygi,data=performans)
sqrt(glance(model)[,1]) #r.squared değerinin karekoku alınır

R değeri bağımlı değişkenin gözlenen ve yordanan değerleri arasındaki korelasyondur.
Bağımlı değişkenin yordanan değerinin bağımlı değişkenin gözlenen değerine mümkün olduğunca yakın olmasını gerektiren en küçük kareler kriterinden dolayı bağımlı değişkenin gözlenen ve yordanan değerleri arasındaki korelasyon eksi değerler alamaz. Dolayısıyla çoklu korelasyon katsayısı 0 ile 1 arasında değişir

Çoklu Korelasyon Formulu \[R_{Y_{12}}= \sqrt{\frac{r^2_{Y_1}+r^2_{Y_2}-2r^2_{Y_1}r^2_{Y_2}r_{12}}{1-r_{12}}}\] \[R_{Y_{12}}=\sqrt{\frac{(0.824)^2+(-0.241)^2-2*(0.824)(-0.241)(0.147)}{1-(0.147)^2}}) = 0.902\]

model_s <- augment(model,data=performans)
cor(model_s[,1], model_s[,5]) # Y ve Y' arası korelasyon

             .fitted
Performans 0.9019952

öğrencilerin gözlenen performans puanları ve yoradan performans puanları arasındaki korelasyon katsayısı nokta 0.902 eşittir

9 Belirlilik Katsayısı

model <- lm(Performans ~ Motivasyon + Kaygi,data=performans)
glance(model)[,1]

Performans puanlarındaki varyansın yaklaşık %81’i öğrencilerin motivasyon ve kaygı puanları tarafından açıklanabilir.

Modele yeni bir bağımsız değişken eklendiğinde, $R^2$ değeri artar, sadece şans eseri olsa bile. Böylece daha fazla bağımsız değişken içeren model sadece daha fazla bağımsız değişken içerdiği için veriye daha iyi uyum sağlıyor gibi gözükebilir.
$\text{adj}{R^2}$ değeri, $R^2$ değerinin modeldeki bağımsız değişken sayısı için modifiye edilmiş versiyonudur. $\text{adj}{R^2}$ değeri, yeni eklenen bağımsız değişken modeli şans eseri beklenenden daha fazla geliştirirse artar, daha az geliştirirse azalır.
$\text{adj}{R^2}$ değeri, eksi değerler alabilir ancak genellikle artı değerler alır. Her zaman $R^2$ değerinden daha düşüktür.
$R^2$ değeri, $n$ gözlemlerin sayısı, $k$ bağımsız değişkenlerin sayısı olmak üzere, aşağıdaki eşitlikle hesaplanabilir. \[R^2_{adj}= R^2 - \frac{k-(1-R^2)}{n-k-1}\] \[R^2_{adj}= 0.814 - \frac{2-(1-0.814)}{15-2-1} =0.783\]

glance(model)[,2]

$adj R^2$ evrende gerçek korelasyonun karesinin daha az yanlı kestirimi olsa da, çoğunlukla $R^2$ değeri rapor edilir.

10 Kestirimin standart hatası

Kestirimin standart hatası (standard error of the estimation), modeldeki artıkların karelerinin toplamının, $n-p$ ( $n$ örneklem büyüklüğü ve $p$ modeldeki parametrelerin sayısı) ile bölünmesiyle elde edilen bölümün kareköküdür.

res <- model$residuals
model_s

sqrt(sum((res - mean(res)) ^ 2 / (length(res)-3)))

[1] 3.650458

glance(model)[,3]

11 Model veri uyumu

Modelin veriye iyi uyup uymadığının test edilmesinde kullanılacak F değeri varyans analizi sonucunda elde edilir.

glance(model)[,4:6] %>% kable(digit=3)

statistic	p.value	df
26.188	0	2

F istatistiği 26.2 değerine eşittir ve istatistiğe ilişkin p < 0.001. Bu olasılık 0.05’ten küçük olduğundan, sıfır hipotezi reddedilir.
Bu sonuç motivasyon ve kaygı değişkenlerinin ikisi birlikte kullanıldığında, çoklu korelasyon katsayısının anlamlı olarak sıfırdan büyük olduğunu ifade etmektedir. Diğer bir ifadeyle, motivasyon ve kaygı değişkenleri performansı istatistiksel olarak anlamlı bir şekilde yordamaktadır.
Regresyon modeli veriye iyi uyum sağlamaktadır.
Model sonuçları

tidy(model) %>% kable(digit=3)

term	estimate	std.error	statistic	p.value
(Intercept)	1.744	5.096	0.342	0.738
Motivasyon	0.686	0.098	6.975	0.000
Kaygi	-0.607	0.207	-2.936	0.012

Performans puanlarındaki farklılıkların bir kısmı motivasyon puanlarındaki farklılıklardan, bir kısmı ise kaygı puanlarındaki farklılıklardan kaynaklanmaktadır

12 Kaygının sabit tutulması

Performansın sadece kaygıdan yordandığı basit regresyon analizi gerçekleştirilirse, yordanan puanlar ve gözlenen puanlar arasındaki fark (artıkPER1), performansın kaygıdan yordanamayan kısmı olacaktır.

artıkPER1 <- lm(Performans ~  Kaygi,data=performans)$residuals

Motivasyonun sadece kaygıdan yordandığı basit regresyon analizi gerçekleştirilirse, yordanan puanlar ve gözlenen puanlar arasındaki fark (artıkMOT), motivasyonun kaygıdan yordanamayan kısmı olacaktır.

artıkMOT <- lm(Motivasyon  ~  Kaygi,data=performans)$residuals

Böylece artıkPER1 ve artıkMOT olarak adlandırılan artık puanlar kaygıdan bağımsız olacaktır.
Diğer bir ifadeyle, kaygı ilişkilerinde herhangi bir rol oynamayacaktır. artıkPER1 puanları artıkMOT puanlarından yordanırsa, artıkMOT puanlarına ilişkin eğim katsayısı 0.686 olarak kestirilecektir. Bu değer, öğrencilerin kaygı düzeyleri kontrol altına alındıktan sonra, motivasyon düzeylerindeki bir birimlik artışın matematikteki performans düzeylerini 0.686 birim artırmaya eğilimli olduğunu önermektedir

lm(artıkPER1  ~  artıkMOT,
   data=data.frame(artıkPER1,artıkMOT))$coefficients %>% kable(digit=3)

	x
(Intercept)	0.000
artıkMOT	0.686

\[B_{Y_{12}} = \frac{r_{Y1}-r_{Y2}r_{12}}{1-r^2_{12}}\frac{sd_Y}{sd_1}\]
\[B_{Y_{12}} = \frac{(0.824)-(-0.241)(0.147)}{1-(0.022)}\frac{7.827}{10.025} = 0.879 * 0.780 =0.686\]
Bu değer, kaygı puanı kontrol altına alındıktan sonra, motivasyon puanlarındaki bir birimlik artışın öğrencilerin matematik performansından 0.686 birim artmaya eğilimi olduğunu önermektedir.

((cor(performans)[2,1] - cor(performans)[3,1]*cor(performans)[2,3])/
   (1-cor(performans)[2,3]^2))*(sd(performans$Performans)/sd(performans$Motivasyon))

[1] 0.6862988

13 Motivasyonun sabit tutulması

Performansın sadece motivasyondan yordandığı basit regresyon analizi gerçekleştirilirse, yordanan puanlar ve gözlenen puanlar arasındaki fark (artıkPER2), performansın motivasyondan yordanamayan kısmı olacaktır.

artıkPER2 <- lm(Performans ~  Motivasyon ,data=performans)$residuals

Kaygının sadece motivasyondan yordandığı basit regresyon analizi
gerçekleştirilirse, yordanan puanlar ve gözlenen puanlar arasındaki fark (artıkKAY), kaygının motivasyondan yordanamayan kısmı olacaktır.

artıkKAY <- lm(Kaygi ~  Motivasyon ,data=performans)$residuals

Böylece artıkPER2 ve artıkKAY olarak adlandırılan artık puanlar motivasyondan bağımsız olacaktır. Diğer bir ifadeyle, motivasyon ilişkilerinde herhangi bir rol oynamayacaktır.
artıkPER2 puanları artıkKAY puanlarından yordanırsa, artıkKAY puanlarına ilişkin eğim katsayısı -0.607 olarak kestirilecektir. Bu değer, öğrencilerin motivasyon düzeyleri kontrol altına alındıktan sonra, kaygı düzeylerindeki bir birimlik artışın matematikteki performans düzeylerini 0.607 birim azaltmaya eğilimli olduğunu önermektedir

lm(artıkPER2  ~  artıkKAY,
   data=data.frame(artıkPER2,artıkKAY))$coefficients %>% kable(digit=3)

	x
(Intercept)	0.000
artıkKAY	-0.607

\[ B_{Y_{21}} = \frac{r_{Y2}-r_{Y1}r_{12}}{1-r^2_{12}}\frac{sd_Y}{sd_2} \]

\[B_{Y_{12}} = \frac{(-0.241)-(0.824)(0.147)}{1-(0.022)}\frac{7.827}{4.769}=(-0.370)*(1.641) =-0.607\]

Bu değer, motivasyon puanı kontrol altına alındıktan sonra, kaygı puanlarındaki bir birimlik artışın öğrencilerin matematik performansından 0.607 birim azaltmaya eğilimli olduğunu önermektedir.

((cor(performans)[3,1] - cor(performans)[2,1]*cor(performans)[2,3])/
   (1-cor(performans)[2,3]^2))*(sd(performans$Performans)/sd(performans$Kaygi))

[1] -0.6072857

14 Regresyon Sabiti

\[ B_0 = M_Y - B_{Y12}*M_1 -B_{Y21}*M_2 \] \[B_0 = 18.176 - (0.686)*(39.933) -(-0.607)*(18.701) = 1.744\]

mean(performans$Performans)-
  model$coefficients[2]*mean(performans$Motivasyon)-
  model$coefficients[3]*mean(performans$Kaygi)

Motivasyon 
  1.744129

Bu değer hem motivasyon puanı hem de kaygı puanı 0’a eşit olduğunda yordanan performans puanıdır.

Böylece yordanan performans puanı

\[Y_{\text{performans}_i} = 1.744 + 0.686 X_{\text{motivasyon}_i} - 0.607 X_{\text{kaygi}_i}\]

15 Standart puanlar ile regresyon

Çoklu regresyon eşitliğini elde etmeden önce değişkenlerin her biri standartlaştırılırsa (değişkenlerin her birinin ortalaması 0, standart sapması 1 olacak şekilde ayarlanırsa), sonuçlar standart sapma birimlerince ifade edilir.

library(QuantPsyc)
lm.beta(model) %>% kable(digit=3)

	x
Motivasyon	0.879
Kaygi	-0.370

Böylece örnekte standartlaştırılmış değişkenler kullanıldığında, yordanan standartlaştırılmış performans düzeyleri aşağıdaki eşitlikle hesaplanabilir:

\[Y_{Zperformans_i} = 0.879 X_{Zmotivasyon_i} + -0.370 X_{Zkaygi_i}\]

Motivasyonun standartlaştırılmış eğim katsayısının mutlak değeri, kaygının standartlaştırılmış eğim katsayının mutlak değerinden daha büyük olduğundan, motivasyonun öğrencilerin matematikteki performanslarını yordamada kaygıya göre daha önemli bir yordayıcı olduğu söylenebilir.

|0.879| > |-0.307|

Ancak bağımsız değişkenlerin standartlaştırılmamış eğim katsayılarını karşılaştırmak uygun değildir.
NOT: Bağımsız değişkenler arasında korelasyon olduğunda, standartlaştırılmış eğim katsayısı bağımlı değişken ile bağımsız değişken arasındaki korelasyon katsayısı değildir.

16 Yordanan ve Artık Değerler

Öğrencilerin standratlaştırılmamış yordanan matematik performans düzeyleri ve standartlaştırılmamış artıkları modelden çekilebilir.

data.frame(
  gercek = performans$Performans,
  yordanan = model$fitted.values,
  artik = model$residuals) %>% kable(digit=3)

gercek	yordanan	artik
12.371	7.461	4.910
4.112	6.869	-2.757
21.627	24.750	-3.123
24.921	22.949	1.972
26.088	26.804	-0.716
17.701	22.416	-4.715
10.272	11.837	-1.565
18.898	22.384	-3.485
19.200	15.558	3.642
17.751	18.013	-0.262
35.501	27.692	7.809
18.041	19.201	-1.160
11.358	10.658	0.701
24.256	24.502	-0.246
10.542	11.546	-1.004

Örneğin, ilk öğrenci için standratlaştırılmamış yordanan değer yaklaşık 7.46, artık ise yaklaşık 4.910’tir.

16.1 Yordanan ve Artık Değerlerin Standart Puanları

library(outliers)
yordanan_s <- model$fitted.values %>% scores(type = "z")
artik_s <- model$residuals %>% scores(type = "z")
data.frame(yordanan_s,artik_s)  %>% kable(digit=3)

yordanan_s	artik_s
-1.518	1.453
-1.601	-0.816
0.931	-0.924
0.676	0.584
1.222	-0.212
0.601	-1.395
-0.898	-0.463
0.596	-1.031
-0.371	1.078
-0.023	-0.077
1.348	2.311
0.145	-0.343
-1.065	0.207
0.896	-0.073
-0.939	-0.297

Öğrencilerin standratlaştırılmış yordanan matematik performans düzeyleri ve standartlaştırılmış artıkları modelden çekilebilir.

library(car)
avPlots(model)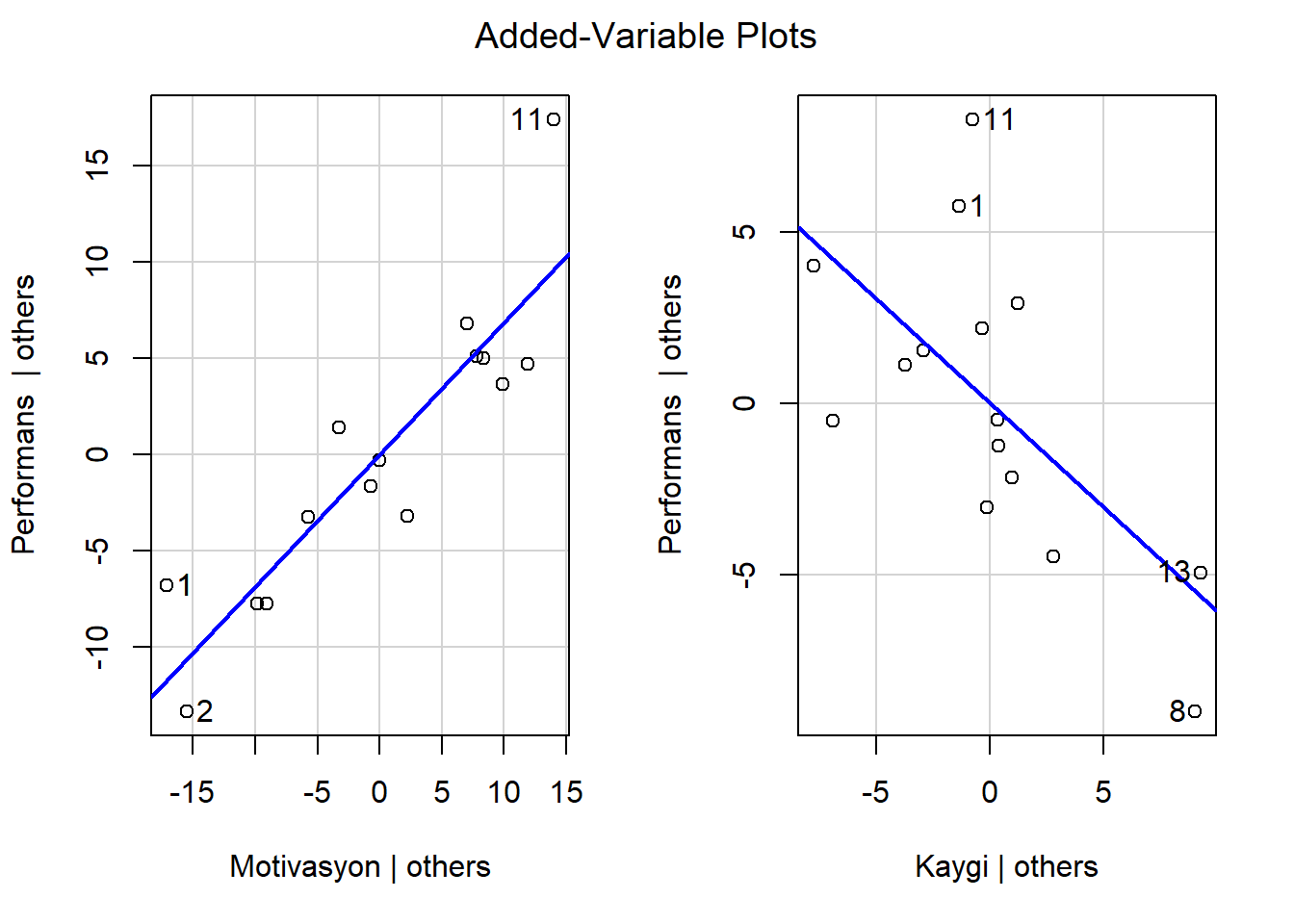

17 Model Grafikleri

Model grafikleri dört farklı şekilde göstermektedir:

Artıklar ve Yordanan Değerler: Doğrusal ilişki varsayımlarını kontrol etmek için kullanılır. Belirgin desenleri olmayan yatay bir çizgi, doğrusal bir ilişkinin göstergesidir.

Normal Q-Q. Artıkların normal dağılıp dağılmadığını incelemek için kullanılır. Artık noktalarının düz kesikli çizgiyi takip etmesi beklenir.

Ölçek-Konum (veya Yayılma-Konum). Artıkların varyansının homojenliğini (homoscedasticity) kontrol etmek için kullanılır. Eşit yayılmış noktalara sahip yatay çizgi, homoscedasticity’nin iyi bir göstergesidir.

Artıklar ve Kaldıraç/Leverage Etkili gözlemleri, yani analize dahil edildiğinde veya analizden çıkarıldığında regresyon sonuçlarını etkileyebilecek uç değerleri belirlemek için kullanılır.

opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(model, las = 1)      # Residuals, Fitted, ...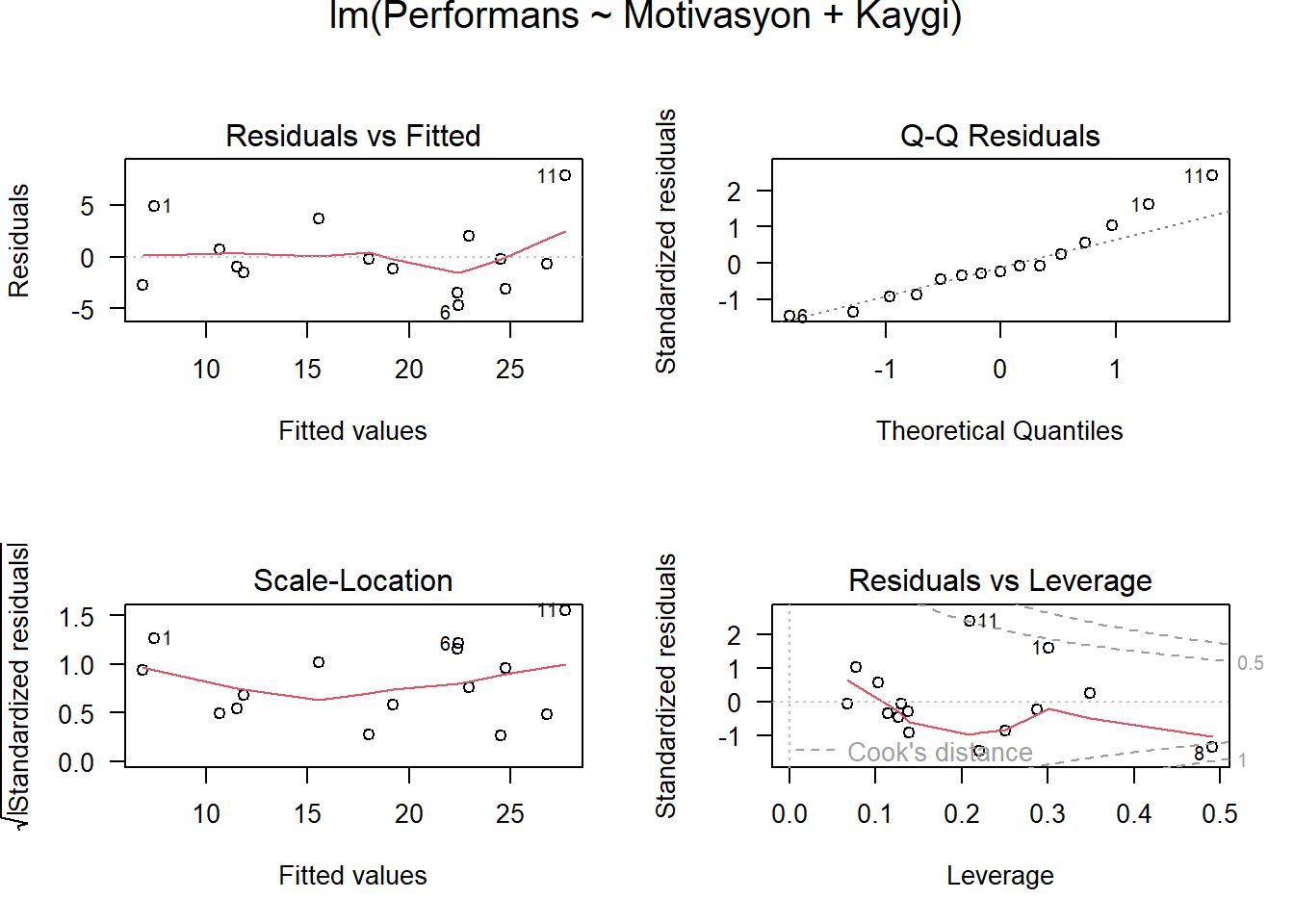

par(opar)

Model grafiklerini daha düzgün elde etmek için ggfortify pakeini de kullanabilirsiniz.

library(ggfortify)
autoplot(model)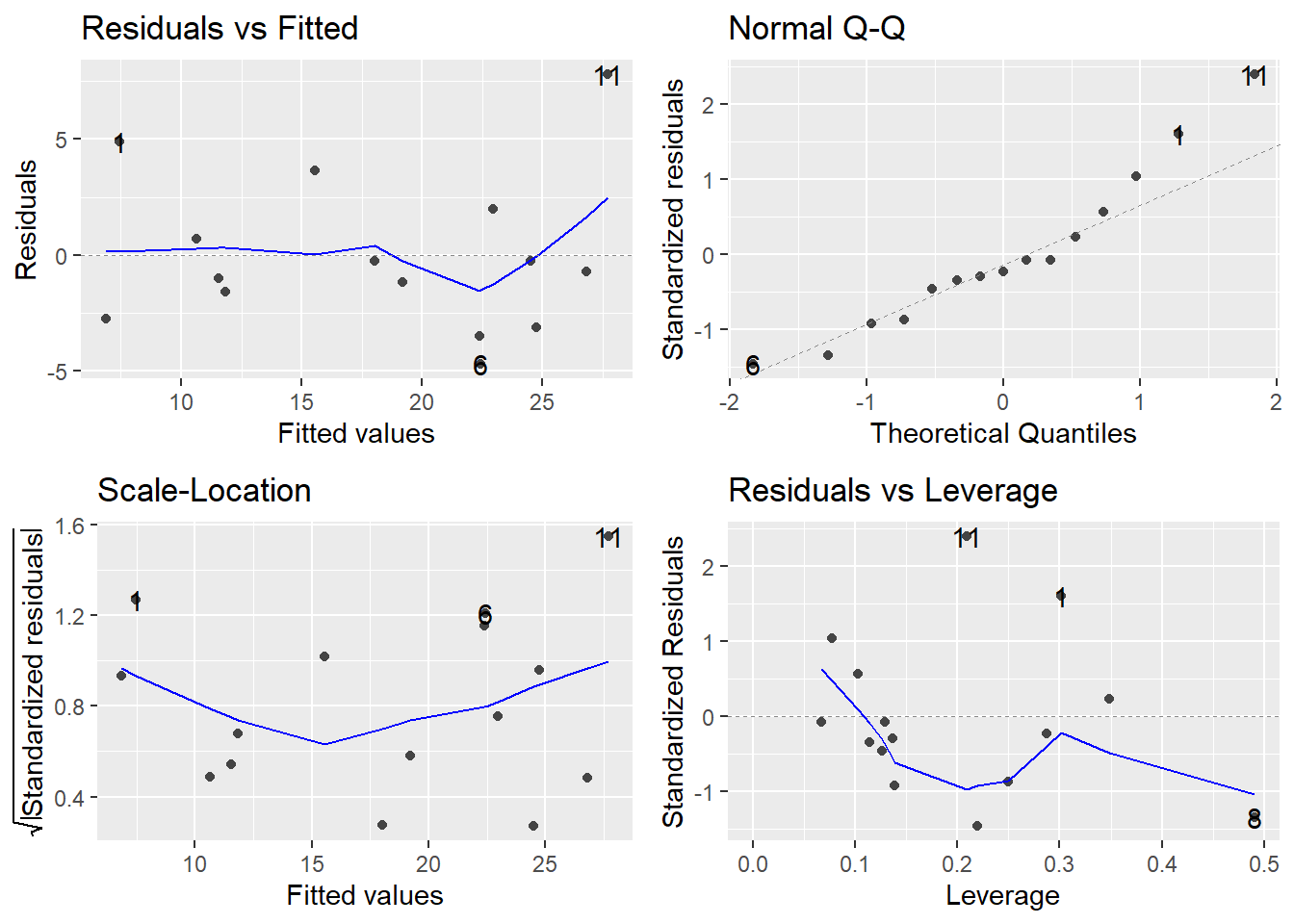

18 Çoklu Regresyon

Regresyon katsayılarından her birinin istatistiksel olarak sıfırdan farklı olup olmadığı test edilebilir. Bu durumda regresyon katsayılarına ilişkin test edilecek sıfır hipotezleri aşağıdaki gibidir:

$H_0: \beta_1 = 0$ - Kaygı düzeyleri eşit olan öğrenciler için motivasyon düzeylerindeki farklılıklar performans düzeylerinde farklılığa yol açmaz.

$H_0: \beta_2 = 0$ - Motivasyon düzeyleri eşit olan öğrenciler için kaygı düzeylerindeki farklılıklar performans düzeylerinde farklılığa yol açmaz.

Hipotez testlerine ilişkin t istatistiği, standartlaştırılmamış regresyon katsayılarının standart hatalarına bölünmesi ile hesaplanır.

tidy(model) %>% kable(digit=3)

term	estimate	std.error	statistic	p.value
(Intercept)	1.744	5.096	0.342	0.738
Motivasyon	0.686	0.098	6.975	0.000
Kaygi	-0.607	0.207	-2.936	0.012

0.686 /0.0984

[1] 6.971545

Motivasyona ilişkin eğim için testin, olasılık değeri (p ˂ 0.001) 0.05’ten daha küçük olduğundan, anlamlı olarak sıfırdan farklı olduğu görülmektedir.
Hipotez testlerine ilişkin t istatistiği standartlaştırılmamış regresyon katsayılarının standart hatalarına bölünmesi ile hesaplanır.
Kaygıya ilişkin eğim de anlamlıdır (t = -2.936, p = 0.012), öğrencilerin motivasyon düzeylerindeki farklılıklar kontrol altına alınsa bile, öğrencilerin kaygı düzeyleri performans düzeylerinde fark yapmaktadır ve kaygı düzeyi negatif bir etkiye sahiptir.
Hipotez testlerine ilişkin t istatistiği standartlaştırılmamış regresyon katsayılarının standart hatalarına bölünmesi ile hesaplanır.
Regresyon katsayısının standart hatası tekrarlanan örneklemlerde istatistiğin değişkenliğini belirtir.
İki regresyon katsayısı ile ilgili p değerleri 0.05 alfa düzeyinden daha küçüktür, bu nedenle her iki bağımsız değişken de öğrencilerin matematikteki performanslarını yordamada istatistiksel olarak anlamlıdır.

19 Yol Şeması

Çoklu regresyon modelini bir yol şeması ile sunmak oldukça kullanışlıdır.

# path model
library(lavaan)
library(lavaanPlot)
model_1 <- 'Performans ~  Motivasyon + Kaygi'
fit1 <- sem(model_1, data = performans)

Standart çözüm

lavaanPlot(model = fit1, coefs = TRUE, stand = TRUE, sig = 0.05)

Standart olmayan çözüm:

Not: Araştırmacılar özellikle ortalamaların yapısı ile ilgilenmedikleri sürece yol şemasında $b_0$ gösterilmez.

lavaanPlot(model = fit1, coefs = TRUE, stand = FALSE, sig = 0.05)

Yol şemeasını istediğiniz formata getirebilirsiniz.

library(semptools)
library(semPlot)
m <- matrix(c("Motivasyon", NA, "NA",  NA,   NA,
                NA, NA, NA,  NA, "Performans",
              "Kaygi",    NA, NA,  NA,   NA), byrow = TRUE, 3, 5)


yol<- semPaths( fit1,  whatLabels = "std",
           sizeMan = 10,
           edge.label.cex = 1.15,
           style = "ram",
           nCharNodes = 0, nCharEdges = 0,
           layout = m)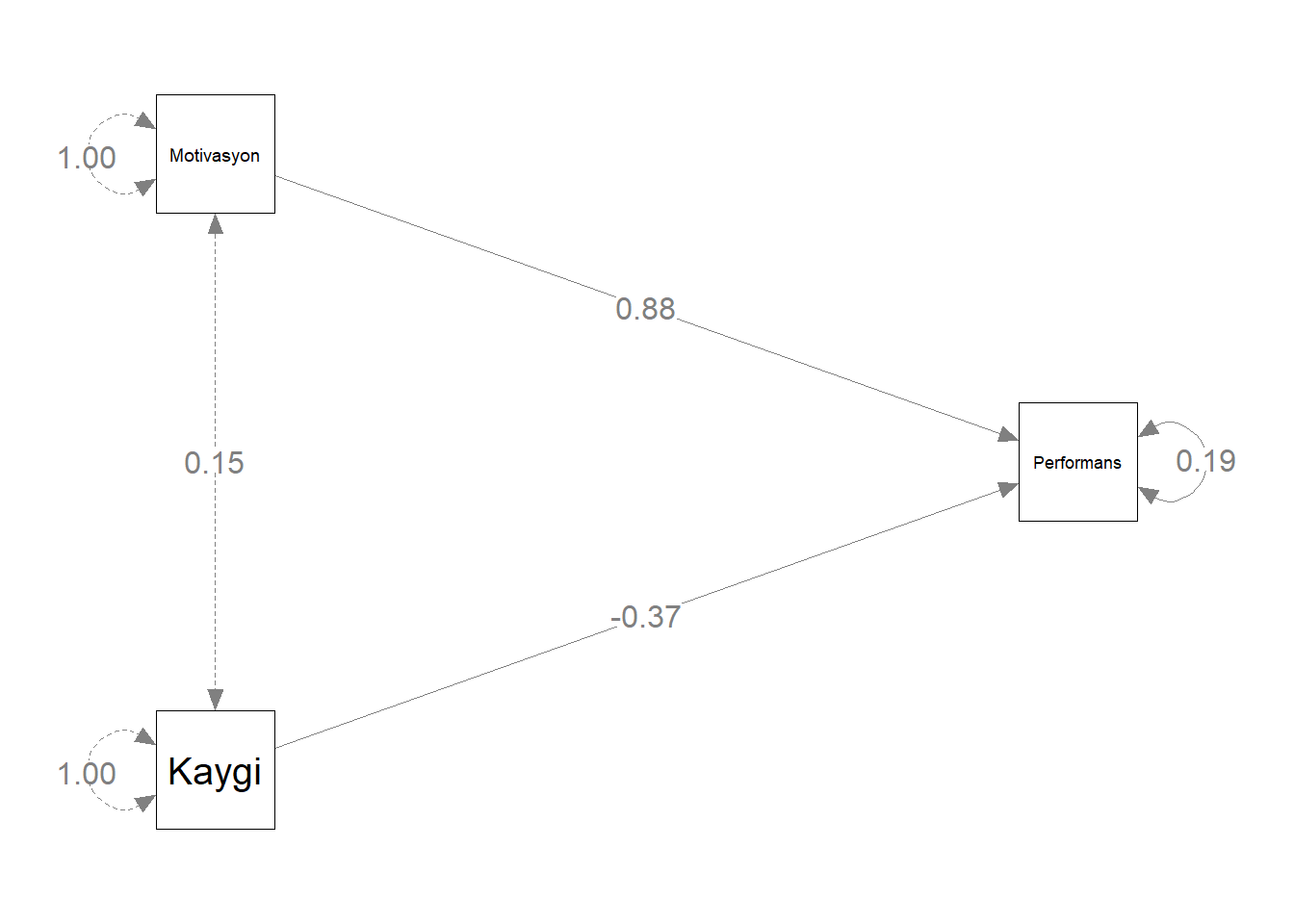

Anlamlılık düzeylerini ekleyebilirsiniz.

yol <- mark_sig(yol, fit1)

plot(yol)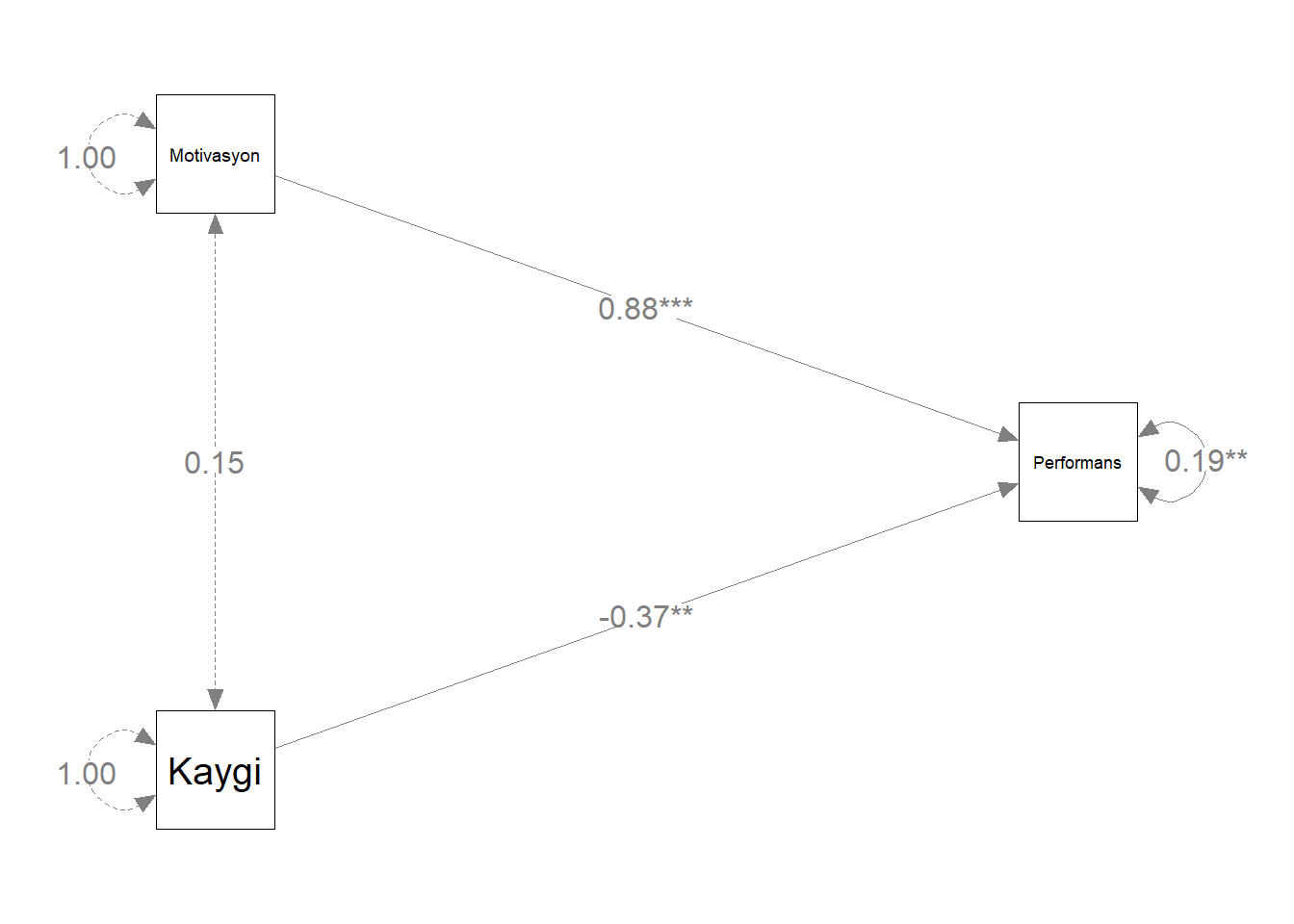

Öğrencilerin matematik performanslarının düzeyini motivasyon ve kaygı düzeylerinden yordamak için çoklu regresyon analizi gerçekleştirilmiştir. Genel regresyon istatistiksel olarak anlamlıdır $F_{[2, 12]} = 26.188, p < .001$ ve $R^2 = 0.814$ Öğrencilerin hem motivasyonlarının düzeyi ( $b_1 = 0.686$) hem kaygılarının düzeyi ( $b_2 = -0.607$) matematik performanslarının düzeyinin istatistiksel olarak anlamlı yordayıcılarıdır, $t = 6.975; p < .001, t = -2.936; p = .012$

20 Aşamalı (Stepwise) Regresyon

Bir regresyon modeline dahil edilebilecek çok sayıda değişken bulunduğunda, bu değişkenlerden en uygun regresyon eşitliğinin oluşturulması için değişken seçiminde çeşitli yöntemler vardır. Bu yöntemlerden birisi aşamalı stepwise regresyondur.
Aşamalı regresyon yöntemi her bağımsız değişkenin regresyon modeline katkısının incelenmesini sağlar.
Bu yönteme göre önce bağımlı değişkenle en yüksek korelasyona sahip bağımsız değişken seçilerek basit regresyon modeli kurulur.
Birinci regresyon eşitliğinden kalan hata varyansının istatistiksel olarak anlamlı kısmını en çok açıklayan bağımsız değişkeni bulmak için kısmi korelasyon katsayıları incelenir ve en yüksek kısmi korelasyon katsayısına sahip bağımsız değişken modele eklenir.
İki bağımsız değişken ile regresyon eşitliği yeniden hesaplanır ve eklenen değişkenin modele anlamlı katkısı olup olmadığı test edilir. Bu işlem modele anlamlı katkı sağlayacak değişken kalmayana kadar devam eder.

tekdegisken <- lm(Performans ~ Motivasyon, data=performans)
glance(tekdegisken) %>%  kable(digit=3)

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.68	0.655	4.598	27.585	0	1	-43.094	92.188	94.312	274.791	13	15

tum  <- lm(Performans ~  Motivasyon + Kaygi, data=performans)
glance(tum) %>%  kable(digit=3)

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
0.814	0.783	3.65	26.188	0	2	-39.033	86.067	88.899	159.91	12	15

Birinci modelde motivasyon tek yordayıcıdır ve performans ile korelasyonu 0.824’tür $R = 0.824$ . Motivasyon tek başına performans puanlarındaki varyansın yaklaşık %68’ini $R^2 = 0.680$ açıklamaktadır.
Modele kaygının yordayıcı olarak eklenmesiyle korelasyon 0.902’ye $R = 0.902$ yükselmiştir. Motivasyon ve kaygı birlikte performans puanlarındaki varyansın yaklaşık %81’ini $R^2 = 0.814$ açıklamaktadır.
Modele kaygının eklenmesiyle $R^2$ değişimi (R Square Change) 0.134’tür. $R^2$ değerindeki bu değişim kaygının eklenmesiyle açıklanan varyans oranında %13’lük bir artış olduğu anlamındadır. $R^2$ değişimi F testi (F Change) ile test edilmiştir ve F değerindeki değişim istatistiksel olarak anlamlıdır $p = 0.012$ Dolayısıyla modele eklenen kaygı değişkeni yordamayı anlamlı olarak geliştirmiştir.

tidy(anova(tum,tekdegisken))

Modelde tek bir yordayıcı (motivasyon) varken, korelasyon 0.824’tür ve sıfır hipotezi doğruysa bu kadar yüksek bir korelasyon elde etme olasılığı p < 0.001. Bu olasılık 0.05’ten küçük olduğundan, korelasyonun anlamlı olarak sıfırdan büyük olduğu söylenebilir.
Modele motivasyon değişkeninin yanı sıra kaygı değişkeni de yordayıcı olarak eklendiğinde, çoklu korelasyon 0.902’dir ve sıfır hipotezi doğruysa bu kadar yüksek bir korelasyon elde etme olasılığı p < 0.001. Bu olasılık 0.05’ten küçük olduğundan, çoklu korelasyonun anlamlı olarak sıfırdan büyük olduğu söylenebilir.
Birinci modelde motivasyon tek yordayıcıdır. Bu modelde motivasyona ilişkin standartlaştırılmamış eğim katsayısı 0.644 olarak kestirilmiş olup kestirimin standart hatası 0.123’tür. Bu katsayı p ˂ .05’te anlamlıdır. Standartlaştırılmış eğim katsayısı 0.824 olarak kestirilmiştir ve bu değer motivasyon ile performansarasındaki korelasyondur.
İkinci modelde motivasyon ve kaygı yordayıcılardır. Bu modelde motivasyona ilişkin standartlaştırılmamış eğim katsayısı 0.686 olarak kestirilmiş olup kestirimin standart hatası 0.098’dir.
Öğrencilerin kaygı düzeyi kontrol altına alındığında, artan motivasyon düzeyi daha yüksek performans puanları ile ilişkilidir. Bu katsayı p ˂ .05’te anlamlıdır. Standartlaştırılmış eğim katsayısı 0.879 olarak kestirilmiştir. Kaygıya ilişkin standartlaştırılmamış eğim katsayısı -0.607 olarak kestirilmiş olup kestirimin standart hatası 0.207’dir. Öğrencilerin motivasyon düzeyi kontrol altına alındığında, artan kaygı düzeyi daha düşük performans puanları ile ilişkilidir.
Kaygının modele eklenmesi korelasyonu çok fazla artırmasa da istatistiksel olarak anlamlı bir yordayıcıdır. Standartlaştırılmış eğim katsayısı -0.370 olarak kestirilmiştir.

21 Etkili Gözlemlerin Belirlenmesi

Etkili gözlemler (influential observations) regresyon sonuçları üzerinde orantısız etkisi olan bütün gözlemleri içerir.
Bu aşırı değerler regresyon doğrusunu kendilerine doğru çekerek modelin katsayıları üzerinde anlamlı etkileri olan değerlerdir.

Regresyon analizinin sonuçları ve sonuçların genellenebilirliği birkaç gözlemle değişebilir. Dolayısıyla bu gözlemlerin etkilerinin değerlendirilmesi için belirlenmesi gerekir.
- En çarpıcı olan (c) grafiğidir. Bu nokta çizgiyi o kadar sert aşağı çekmiş ki, pozitif olan ilişki negatife dönmüş!
- a ve b de değerleri çizgiyi saptırmıyorlar, sadece uzatıyorlar. Bunlar yüksek kaldıraçlıdır ama modele zarar vermezler, hatta ilişkinin gücünü (korelasyonu) yapay olarak artırabilirler.
- Grafik (d): “Tahterevallinin tam ortasına ağır bir yük koymak gibi. Dengeyi bozmuyor (eğimi çok değiştirmiyor) ama çubuğu yukarı itiyor.” (Intercept/Kesişim kayması).
- Grafik (e): Normalde ilişki güçlü (dik). Ama sağdaki siyah noktalar çizgiyi aşağı bastırarak eğimi düzleştirmiş. İlişkiyi olduğundan daha zayıf gösteriyorlar.
- Grafik (f): Siyah nokta o kadar yukarıda ki, çizgiyi kendine çekip eğimi dikleştirmiş. İlişkiyi olduğundan daha şiddetli gösteriyor
Etkili gözlem, gözlemlerdeki veya veri girişindeki bir hatadan kaynaklanabilir. Bu durumda birey analizden çıkarılabilir veya veri düzeltilebilir.
Sıradışı bir durumla açıklanabilen, ender karşılaşılan geçerli bir gözlem analizden çıkarılabilir. Halbuki olası bir açıklaması olmayan, ender karşılaşılan bir gözlemi bir neden olmadan çıkarmak problemlidir ancak gözlemin analize dahil edilmesi de savunulamayabilir. Bu durumda analizlerin gözlem dahil edilerek ve dahil edilmeyerek tekrarlanması önerilir.
Cook’s D
- Etkinin en yaygın ölçümü Cook’s D olarak bilinir.
- Bağımlı değişkenlerdeki potansiyel uç değerlerin belirlenmesinde kullanışlı bir istatistiktir. Uzaklık için en yaygın ölçüm artıktır.
- Artık herhangi bir nokta ve regresyon eğrisi arasındaki dikey uzaklığı ölçer. Bu noktalar rastgele hatayı temsil edebilir, veri yanlış kodlanmış olabilir veya veri setine ait olmayan olağan dışı durumları yansıtabilir.
- Cook’s D i gözlemi veriden çıkarılıp analiz yeniden gerçekleştirilirse, $b_j$ katsayısındaki değişikliğin karesinin toplamının bir fonksiyonudur.
- Her gözlem için hesaplanabilir. Her gözlem için bu değer, N gözlemlerin sayısı olmak üzere 4/N ile karşılaştırılabilir. 4/N üzerindeki değerler problem olabilecek gözlemlere işaret eder.
Cook’s D için kesme noktası $4/15= 0.267$, 1., 8. ve 11. gözlemler bu sınırı asıyor

Cook’s D

library(olsrr)
ols_plot_cooksd_bar(model)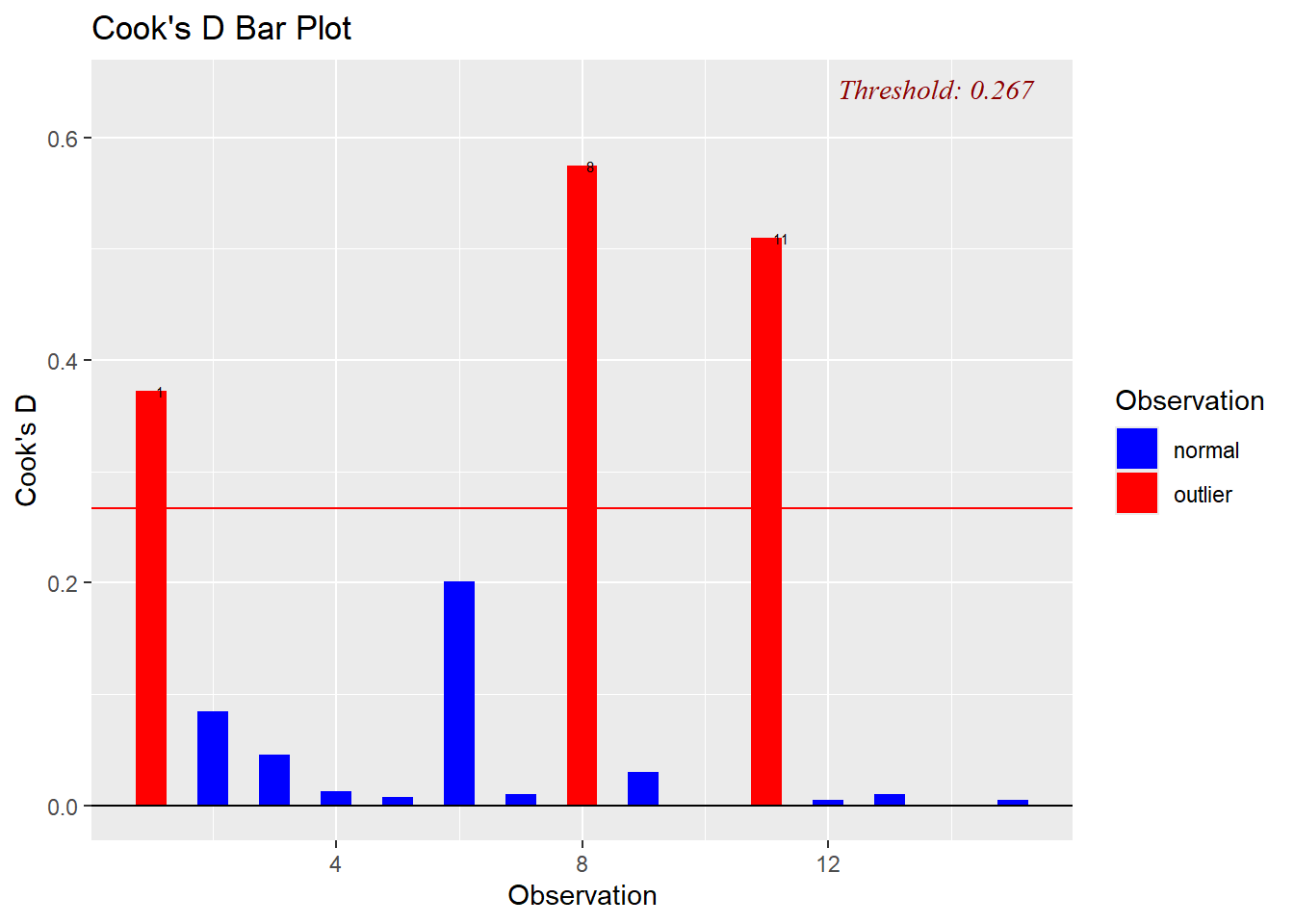

DFBETA

Cook’s D etkinin genel bir ölçümü olarak düşünülebilir. Gözlemin eklenmesiyle her katsayının nasıl değiştiğini ölçen daha spesifik bir ölçüm ele alınabilir. Bu ölçüm DFBETA olarak adlandırılır ve her gözlem için hesaplanabilir. (kritik değer $2/\sqrt{n}$

DFBETA için kesme noktası ise $2/\sqrt{15} = 0.516$ hat değerleri ise levarge a karşılık geliyor.

DFBETA

ols_plot_dfbetas(model)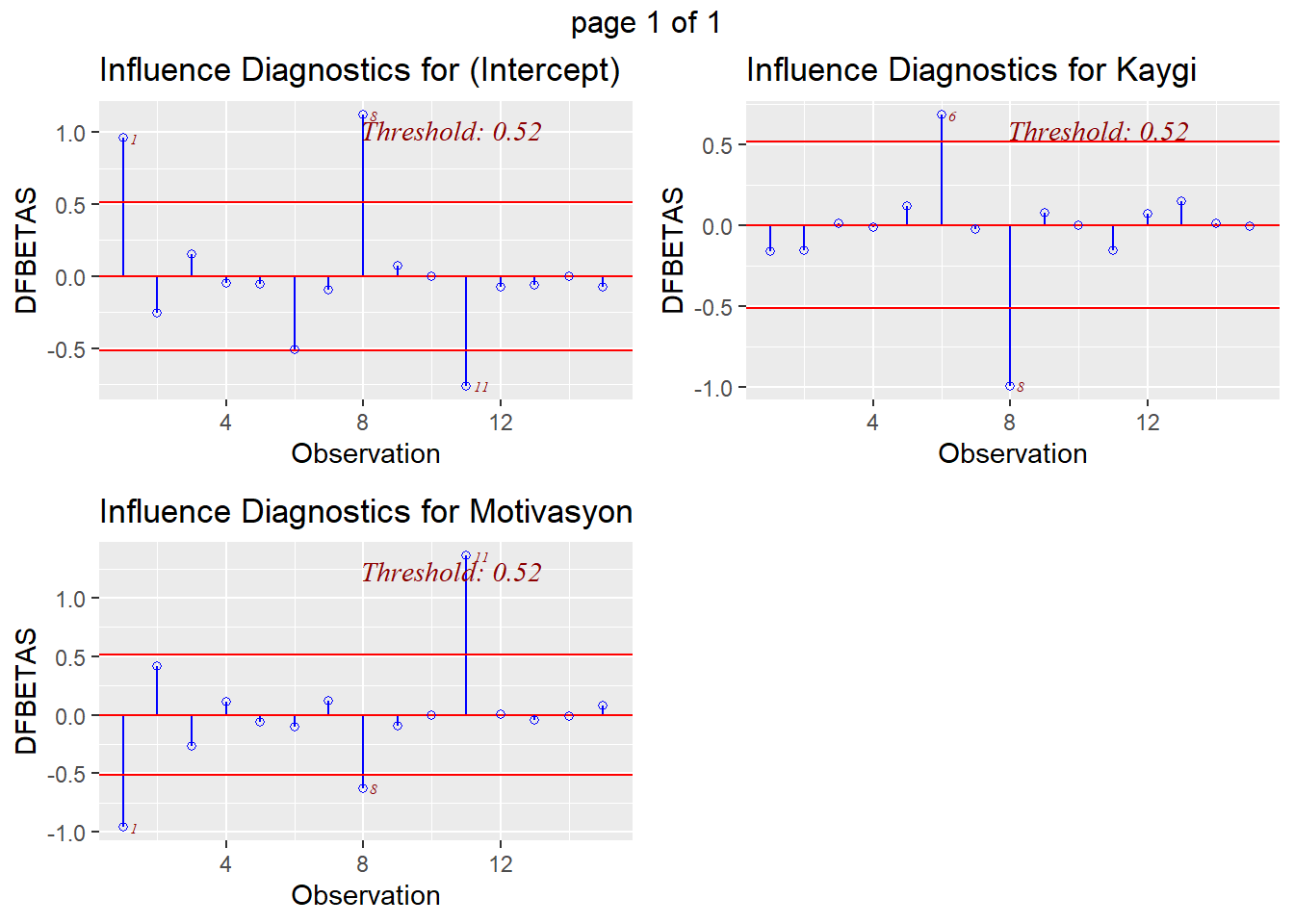

influence.measures(model, infl = influence(model))

Influence measures of
     lm(formula = Performans ~ Motivasyon + Kaygi, data = performans) :

     dfb.1_  dfb.Mtvs dfb.Kayg   dffit cov.r   cook.d    hat inf
1   0.95795 -0.960377 -0.16108  1.1422 0.896 0.372039 0.3012    
2  -0.25252  0.415588 -0.15745 -0.4984 1.422 0.084595 0.2501    
3   0.14949 -0.263213  0.00861 -0.3676 1.209 0.045656 0.1388    
4  -0.04850  0.110703 -0.01220  0.1872 1.332 0.012398 0.1026    
5  -0.05212 -0.059328  0.11625 -0.1413 1.796 0.007232 0.2869   *
6  -0.50564 -0.103904  0.68481 -0.8203 0.924 0.201071 0.2200    
7  -0.09262  0.115511 -0.02600 -0.1686 1.409 0.010150 0.1264    
8   1.12071 -0.626060 -0.99660 -1.3623 1.570 0.574244 0.4905   *
9   0.07075 -0.094818  0.07387  0.3019 1.061 0.030173 0.0774    
10 -0.00254  0.000079 -0.00142 -0.0191 1.390 0.000132 0.0670    
11 -0.76153  1.357765 -0.15466  1.6459 0.228 0.510106 0.2092   *
12 -0.07535  0.006834  0.07308 -0.1166 1.424 0.004897 0.1142    
13 -0.06170 -0.043739  0.14852  0.1670 1.965 0.010089 0.3487   *
14 -0.00051 -0.015642  0.01231 -0.0267 1.490 0.000260 0.1297    
15 -0.07231  0.081208 -0.00672 -0.1135 1.472 0.004648 0.1373

Leverage/Kalıdraç (hi) (b c grafiği gibi)
- Bağımsız değişkenlerdeki potansiyel uç değerlerin belirlenmesinde kullanışlı bir istatistiktir.
- Levarage bir gözlemin bir bağımsız değişkene, $X_j$, göre olağan dışı olma derecesini ölçer.
- Leverage için olası değerler, N gözlemlerin sayısı olmak üzere, 1/N ile 1.0 arasında değişir.
- Ortalama leverage puanı, p bağımsız değişken sayısı ve N gözlem sayısı olmak üzere, (p +1)/N eşitliği ile hesaplanabilir. Yüksek leverage değerine sahip gözlemler ortalama değerden 2 veya 3 kat daha yüksek leverage puanlarına sahip olacaktır.

library(olsrr)
ols_plot_resid_lev(model)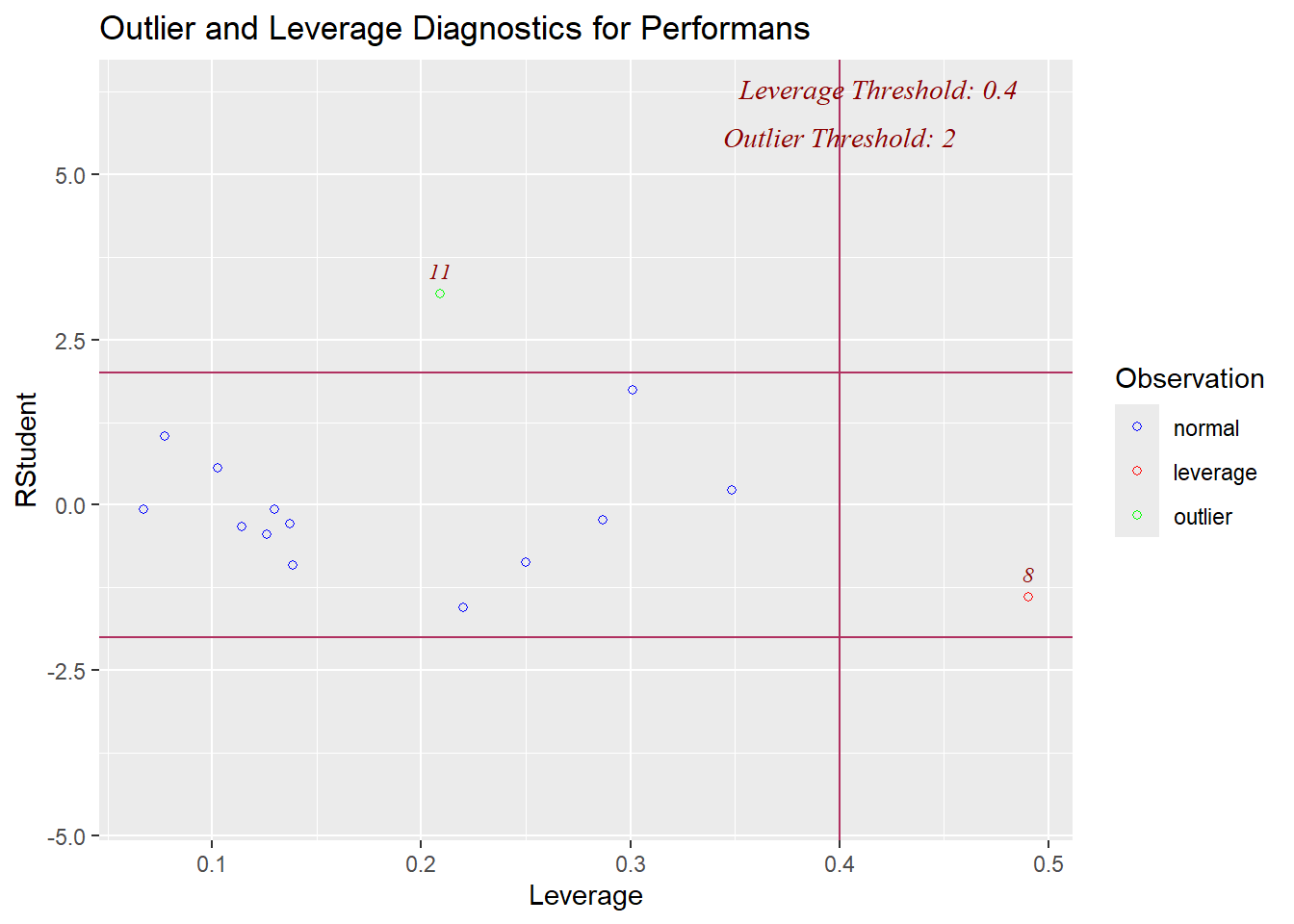

Influence (Etki)
- Etkili bir gözlem uzaklık ve/veya leverage için yüksek değere sahip olan ve modelin kesişim ve eğim katsayılarını anlamlı olarak etkileyen bir gözlemdir.
- Bu gözlemin varlığı veya yokluğu regresyon yüzeyinin yerini önemli ölçüde değiştirecektir.
- Uzaklık ve/veya leverage için yüksek değere sahip gözlemlerin regresyon üzerinde önemli bir etkisi olmayabilir. Bir gözlemin etkide yüksek olması için hem uzaklık hem de leverage için yüksek değerlere sahip olması gerekir.

ols_plot_dffits(model)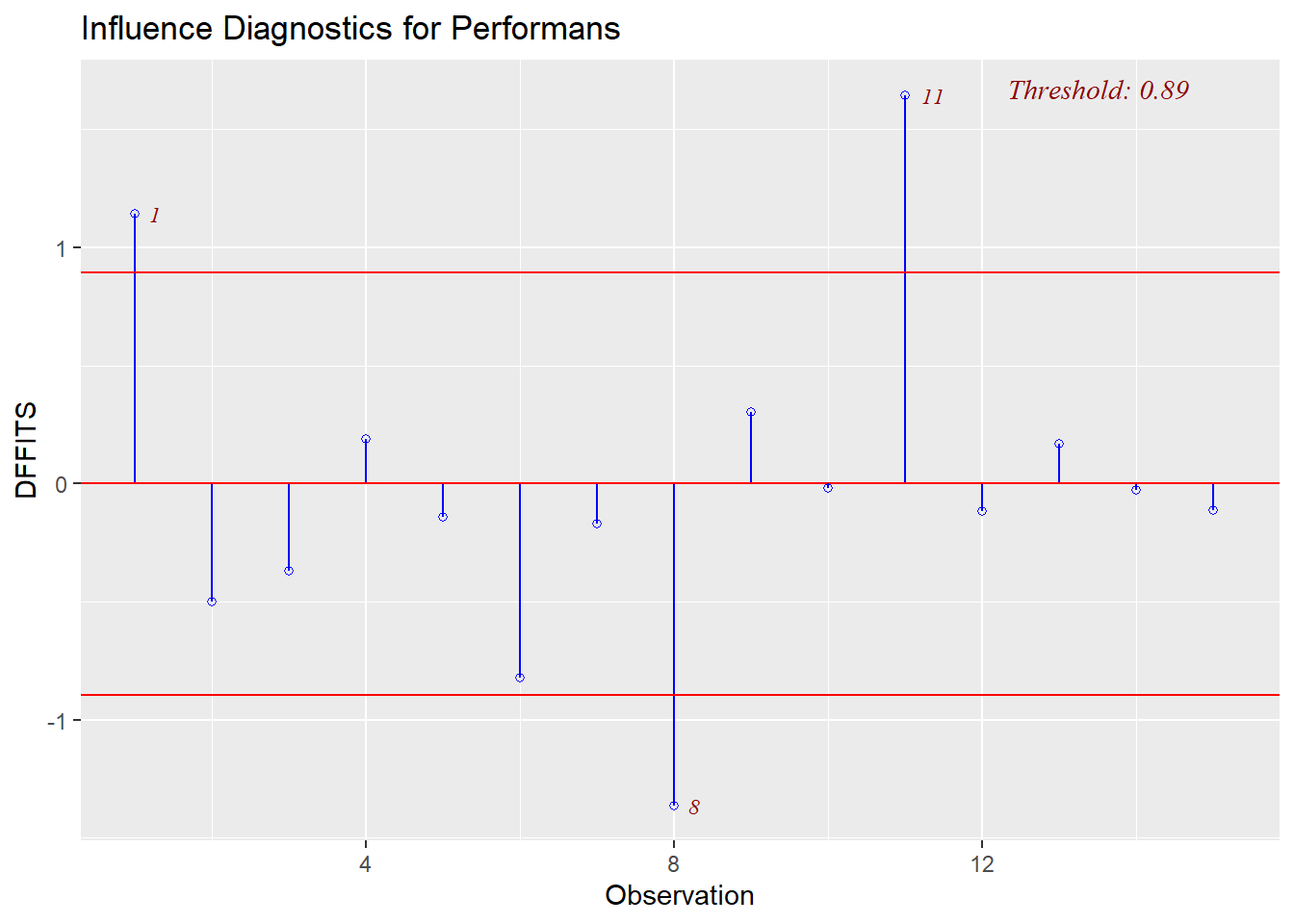

Özetle

Studentized Residuals Aykırı Değer (Outlier) gözlemin model çzigisinden uzaklığı ölçer. standart puan gibi -+3 aralığı dışındaki gözlemleri incelemek gerekir.
Leverage (Hat Values) Kaldıraç Gücü (Leverage) gözlemin bağımsız değişken değerleri içindeki uzaklığı nedir?” Ortalamanın 2-3 katı uzaklarına dikkat etmek gerekir.
Cook’s Distance Toplam Etki “Hem uzakta hem de uçta mı? Modeli tek başına değiştiriyor mu?” 4/n i geçen değerler incelenmeli

22 Kategorik Bağımsız bir Değişken ile Çoklu Regresyon

Regresyon modellerinde bağımsız bir değişken sürekli veya kategorik olabilir.
Bir regresyon analizine kategorik bir değişkeni dahil ederken, regresyon modelinin değişkenin düzeylerindeki farklılıkları doğru olarak kestirmesini saglamak için, değişkenin düzeylerinin yeniden kodlanması gerekmektedir.
Kategorik değişkenleri kodlamanın en basit yöntemi dummy (yapay) kodlamadır.
Dummy kodlama ile kategorik değişkenin düzeylerine sayısal değerler atanarak dummy değişken(ler) oluşturulur.

Dummy değişken kategorik bir değişkenin düzeylerinin sayısal gösterimidir.

Bir bireyin k tane düzeye sahip kategorik bağımsız bir değişkenin belli bir düzeyine ilişkin üyeliğini temsil eden k-1 tane dummy değişken oluşturulur.
Eğer bir birey kategorik değişkenin birinci düzeyindeyse birinci dummy değişkene 1 değeri verilir, birey değişkenin başka bir düzeyindeyse birinci dummy değişkene 0 değeri verilir.
Eğer aynı birey kategorik değişkenin ikinci düzeyindeyse ikinci dummy değişkene 1 değeri verilir, birey değişkenin başka bir düzeyindeyse ikinci dummy değişkene 0 değeri verilir.
Eğer aynı birey kategorik değişkenin (k-1). düzeyindeyse (k-1). dummy değişkene 1 değeri verilir, birey değişkenin başka bir düzeyindeyse (k-1). dummy değişkene 0 değeri verilir.
Böyle bir kodlama ile oluşturulan her bir dummy değişken iki düzeye sahiptir: 1 ve 0
Bir kategorik değişken için oluşturulan dummy değişkenlerle gerçekleştirilen bir regresyon analizinde regresyon katsayılarının yorumlanması aşağıdaki gibidir:
Birinci dummy değişkene ilişkin katsayı, diğer bütün değişkenler kontrol altına alındığında, kategorik değişkenin birinci düzeyi ve kategorik değişkenin son düzeyi arasındaki bağımlı değişkenin yordanan değerinin farkıdır.
İkinci dummy değişkene ilişkin katsayı, diğer bütün değişkenler kontrol altına alındığında, kategorik değişkenin ikinci düzeyi ve kategorik değişkenin son düzeyi arasındaki bağımlı değişkenin yordanan değerinin farkıdır.
j. dummy değişkene ilişkin katsayı, diğer bütün değişkenler kontrol altına alındığında, kategorik değişkenin j. düzeyi ve kategorik değişkenin son düzeyi arasındaki bağımlı değişkenin yordanan değerinin farkıdır.

22.1 Dummy Değişkenlerin Oluşturulması Örnek: Performansın Yordanması

Üç düzeyi (evil, bekar ve diger) bulunan medeni durum değişkeni için biri “Evli”, digeri “Bekar” olarak adlandırılan iki dummy değişken (ornegin, D1 ve D2) oluşturulabilir.

Medeni Durum	D1 (Evli)	D2 (Bekar)	D3 (Diğer)
Evli	1	0	0
Bekar	0	1	0
Diger	0	0	1

Referans Grup: Diğer
Kategorik değişkenin üç düzeyini göstermek için üç gösterge değişkenine ihtiyaç yoktur. değişkenin düzeyleri sadece iki göstergeyle tanımlanmıştır.
D1 değişkeni için 0 değerine, D2 değişkeni için 0 değerine sahip bir birey diğer kategorisine aittir.
D1 ve D2 bağımsız değişkenleri ile gerçekleştirilen bir regresyon analizinde kestirilen $b_1$ eğim katsayısı evliler ve diğerleri arasındaki yordanan matematik performansı farkını, $b_2$ eğim katsayısı ise bekarlar ve diğerleri arasındaki yordanan matematik performansı farkını belirtir.
Evliler ve bekarlar arasındaki yordanan matematik performansi farkı, birinci ve ikinci medeni durum katsayıları arasındaki farktır: $b_1 - b_2$
veri seti 🔗Performansd1.sav

library(haven)
Performansd1 <- read_sav("data/Performansd1.sav")
summary(Performansd1)

   Performans       Motivasyon        Kaygi           Guven      
 Min.   : 4.112   Min.   :22.00   Min.   :10.72   Min.   : 8.75  
 1st Qu.:11.864   1st Qu.:34.00   1st Qu.:15.54   1st Qu.:17.12  
 Median :18.041   Median :40.00   Median :18.30   Median :22.00  
 Mean   :18.176   Mean   :39.93   Mean   :18.07   Mean   :21.63  
 3rd Qu.:22.941   3rd Qu.:47.00   3rd Qu.:18.84   3rd Qu.:25.60  
 Max.   :35.501   Max.   :55.00   Max.   :28.17   Max.   :38.70  
    Medeni         
 Length:15         
 Class :character  
 Mode  :character

library(fastDummies)
# Performansd1$D1 <- ifelse(Performansd1$Medeni  == "Evli", 1, 0)
# Performansd1$D2<- ifelse(Performansd1$Medeni  == "Bekar", 1, 0)
dataf <- dummy_cols(Performansd1, select_columns = 'Medeni')
summary(dataf)

   Performans       Motivasyon        Kaygi           Guven      
 Min.   : 4.112   Min.   :22.00   Min.   :10.72   Min.   : 8.75  
 1st Qu.:11.864   1st Qu.:34.00   1st Qu.:15.54   1st Qu.:17.12  
 Median :18.041   Median :40.00   Median :18.30   Median :22.00  
 Mean   :18.176   Mean   :39.93   Mean   :18.07   Mean   :21.63  
 3rd Qu.:22.941   3rd Qu.:47.00   3rd Qu.:18.84   3rd Qu.:25.60  
 Max.   :35.501   Max.   :55.00   Max.   :28.17   Max.   :38.70  
    Medeni             Medeni_1         Medeni_2         Medeni_3     
 Length:15          Min.   :0.0000   Min.   :0.0000   Min.   :0.0000  
 Class :character   1st Qu.:0.0000   1st Qu.:0.0000   1st Qu.:0.0000  
 Mode  :character   Median :0.0000   Median :0.0000   Median :0.0000  
                    Mean   :0.2667   Mean   :0.4667   Mean   :0.2667  
                    3rd Qu.:0.5000   3rd Qu.:1.0000   3rd Qu.:0.5000  
                    Max.   :1.0000   Max.   :1.0000   Max.   :1.0000

model_dummy <- lm(Performans ~ Medeni_1 + Medeni_2 , 
                  data=dataf)
model_dummy


Call:
lm(formula = Performans ~ Medeni_1 + Medeni_2, data = dataf)

Coefficients:
(Intercept)     Medeni_1     Medeni_2  
    19.6442      -6.6234       0.6386

tidy(model_dummy)

Kesişim katsayısı $b_0$ 19.644 matematik değerine eşittir. Bu değer, medeni durumu diğer olan öğrencilerin yordanan performans puanıdır.
Evli için standartlaştırılmamış eğim katsayısı $b_1$ -6.623 değerine eşittir. Bu değer, evliler ve diğerleri arasındaki yordanan matematik performans puanları farkının -6.623 birim olduğunu önerir.
$19.644 – 6.623 = 13.021$ medeni durumu evli olan öğrencilerin yordanan matematik performans puanıdır.
benzer şekilde, bekar için standartlaştırılmamış eğim katsayısı $b_21$ 0.639 değerine eşittir. Bu değer, bekarlar ve diğerleri arasındaki yordanan matematik performans puanları farkının 0.639 birim olduğunu önerir.
$19.644 + 0.639 = 20.283$ medeni durumu bekar olan öğrencilerin yordanan matematik performans puanıdır.
lm() fonksiyonu ise aşağıdaki şekilde Medeni değişkenini kategorik hale getirmeketdir.

model_2 <- lm(Performans ~ Medeni , 
                  data=Performansd1)
library(broom)
tidy(model_2)

23 Çoklu Regresyonda İki-Yönlü Etkileşim Etkisi

Eğer bir çoklu regresyon modelinde bir bağımsız değişken ile bağımlı değişken arasındaki ilişkinin büyüklüğü diğer bir bağımsız değişkenin düzeyine göre değişirse, etkileşim gözlenir.
Etkileşim etkisi, düzenleyici (moderator) etki olarak da bilinmektedir.
Etkileşim terimi $X_1$ değişkeninin değerlerinin düzenleyici $X_2$ değişkeninin değerleriyle çarpılmasıyla oluşan bileşik bir değişkendir. Regresyon eşitliği aşağıdaki gibidir:

\[Y= a + b_1x_{1i} + b_2x_{2i} + b_3x_{1i}x_{2i}\]

Daha iyi anlaşılması için formülü şu değişkenlerle hayal edelim:

$Y$ (Bağımlı Değişken): Sınav Notu
$X_1$ (Bağımsız Değişken 1): Ders Çalışma Süresi (Saat)
$X_2$ (Düzenleyici Değişken): Derse Olan İlgi (0 = Hiç Yok, 10 = Çok Yüksek)

Denklemimiz:

$$Not = a + b_1(\text{Süre}) + b_2(\text{İlgi}) + b_3(\text{Süre} \times \text{İlgi})$$

$b_3$ Katsayısı (Etkileşim/Interaction Etkisi)

$X_2$’deki bir birimlik artışın, $X_1$ ile $Y$ arasındaki ilişkinin eğiminde (slope) yarattığı değişimdir. “Bu katsayı bize ‘Duruma göre değişir’ demenin matematikçesidir. $b_3$ şunu söyler: ‘Ders çalışma süresinin notuna etkisi, derse ne kadar ilgi duyduğuna bağlı olarak artar veya azalır.’”
- Pozitif çıkarsa: İlgi arttıkça, çalışmanın not üzerindeki etkisi daha da güçlenir (Kaldıraç etkisi).
- Negatif çıkarsa: İlgi arttıkça, çalışmanın etkisi azalır.

$b_1$ Katsayısı ($X_1$’in Basit Etkisi )

Dikkat “Çalışmanın nota etkisi” değil

$X_2$ (İlgi) SIFIR olduğunda, $X_1$’deki (Süre) bir birimlik artışın $Y$’de yarattığı değişimdir. “Bu katsayı, sadece ve sadece derse ilgisi 0 olan (hiç ilgisi olmayan) öğrenciler için geçerlidir. Sadece ilgisiz bir öğrenci 1 saat fazla çalışırsa notu $b_1$ kadar artar. İlgisi yüksek olanlar için bu katsayı tek başına yetersizdir.”

$b_2$ Katsayısı ($X_2$’nin Basit Etkisi)

$X_1$ (Süre) SIFIR olduğunda, $X_2$’deki (İlgi) bir birimlik artışın $Y$’de yarattığı değişimdir. “Bu katsayı, kitabı hiç açmayan (Çalışma süresi = 0 olan) bir öğrenci için geçerlidir. Hiç çalışmasan bile, sadece derse ilgi duymak notunu $b_2$ kadar artırır.”

$a$ (Sabit / Intercept)

Hem $X_1$ hem de $X_2$ sıfır olduğunda $Y$’nin alacağı değer. “Hem hiç çalışmadın ($X_1=0$) hem de derse hiç ilgin yok ($X_2=0$). Sınavdan alacağın taban puan budur.”

“Normal regresyonda ($b_1$ ve $b_2$ varken) musluğu açarsanız su akar.

Etkileşim ($b_3$) olduğunda ise; $X_2$ değişkeni bir vana görevi görür. Vana kapalıyken ($X_2=0$) musluğu açsanız da az su akar ($b_1$). Ama vanayı sonuna kadar açarsanız ($X_2$ yüksekse), musluğu aynı miktarda çevirdiğinizde tazyikli su akar ($b_1 + b_3$ etkisi). Yani $X_2$, $X_1$’in gücünü ayarlar.”

Sunumdaki örnek Wagner, Compas ve Howell’in (1988) çalışmasından gelmektedir.
Wagner ve diğerleri çalışmalarında daha fazla strese maruz kalan bireylerin psikolojik belirtileri daha yüksek düzeyde göstereceğini önermiştir. Ancak bir birey stresiyle basa çıkmasına yardımcı olacak yüksek düzeyde sosyal desteğe sahipse, belirtilerin stres arttıkça daha yavaş artmasının bekleneceğini, daha az sosyal desteğe sahip bireyler için ise, semptomların stres arttıkça daha hızlı artmasının bekleneceğini belirttiler. veri seti 🔗 Hassles.sav - aşağıda stres sorun olarak isimlendirilmiştir.
“Hassles.sav” SPSS veri dosyası bir ID değişkeni ve ID değişkeni dışında dört değişken ve 56 üniversite birinci sınıf öğrencisini içermektedir.

library(haven)
zorluklar <- read_sav("data/Hassles.sav")[,c(1,2,4,5)]
colnames(zorluklar)  <- c("id","sorun","destek","belirtiler")

İlk olarak değişkenler arasındaki ilişkilere bakılır.

ggpairs(zorluklar[,-1])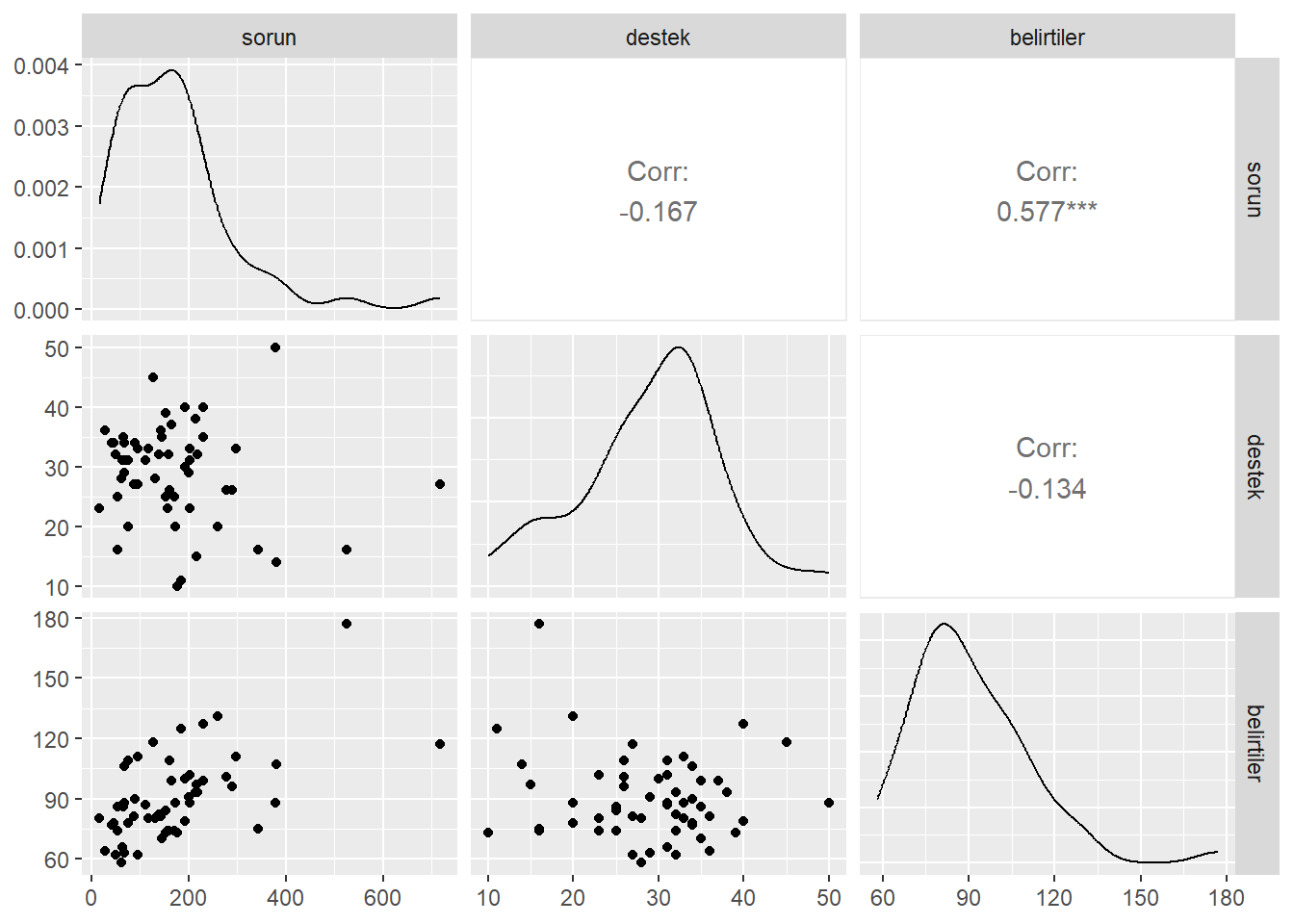

Destek, sorun veya belirtiler ile ilişkili olmamasına rağmen, beklendiği gibi, sorun ve belirtiler arasında istatistiksel olarak bir ilişki vardır (r = 0, 577).
Ancak bu bulgular sorun ve belirtiler arasındaki ilişkinin destek düzeyine bağlı olup olmadığı sorusuna cevap vermemektedir. Sorun ve destek etkileşimini test etmek için sorun değerleri ile destek değerlerinin çarpımıyla yeni bir değişken olusturulur.
Ancak bu iki değişkene ilişkin değerlerin çarpılmasıyla oluşan değişkenin analize dahil edilmesinde iki problem ortaya çıkacaktır.
Sorun veya Destek değişkenlerinden biri veya ikisi, çarpımlarıyla oluşan değişken ile yüksek düzeyde korelasyona sahip olacaktır ki bu da veride çoklu bağlantı problemine neden olacaktir.
Regresyon analizinde sorun veya destek değişkeninin herhangi bir etkisi diğer değişkenin değerinin 0 olduğu durumda değerlendirilecektir. diğer bir ifadeyle, sorun üzerindeki test hiç sosyal desteği olmayan bir katılımcı için Sorunların belirtilerle ilişkili olup olmadığı testi olacaktır.
Benzer şekilde, destek üzerindeki test hiç sorunları olmayan katılımcılar için değerlendirilecektir.
Hem çoklu bağlantı problemi, hem de ana etkilerden birinin diğer ana etkinin uç değerinde değerlendirilmesi problemi istenmeyen durumlardır.
Bahsedilen problemlerle başa çıkmak için sorun değişkeni ve destek değişkeni merkezlenebilir.
Bunun için her bir değişkene ilişkin bireysel gözlemlerden ilgili değişkenin ortalaması çıkarılarak sapma puanları hesaplanacaktır.

zorluklar$csorun <- zorluklar$sorun -mean(zorluklar$sorun)
zorluklar$cdestek <- zorluklar$destek -mean(zorluklar$destek)
zorluklar$cross  <- zorluklar$sorun*zorluklar$destek
zorluklar$cross_m  <- zorluklar$csorun*zorluklar$cdestek

değişkenler merkezlendikten sonra merkezlenen sorun değişkeni için 0 değeri sorun değişkeninin ortalama düzeyindeki katılımcıları temsil ederken, merkezlenen destek değişkeni için 0 değeri destek değişkeninin ortalama düzeyindeki katılımcıları temsil eder.
Böylece ana etkiler diğer değişkenin uygun düzeyinde değerlendirilir.
Değişkenlerin merkezlenmesiyle sorun ve destek değişkenleri arasındaki çoklu bağlantı da önemli ölçüde düşecektir.
Merkezlenen sorun, Merkezlenen destek, Merkezlenen sorun değişkeninin değerleri ile Merkezlenen Destek değişkeninin değerlerinin çarpılmasıyla elde edilen etkileşim terimi ve Belirtiler arasındaki korelasyon matrisi incelenir.

ggpairs(zorluklar[,c(2:4,7)])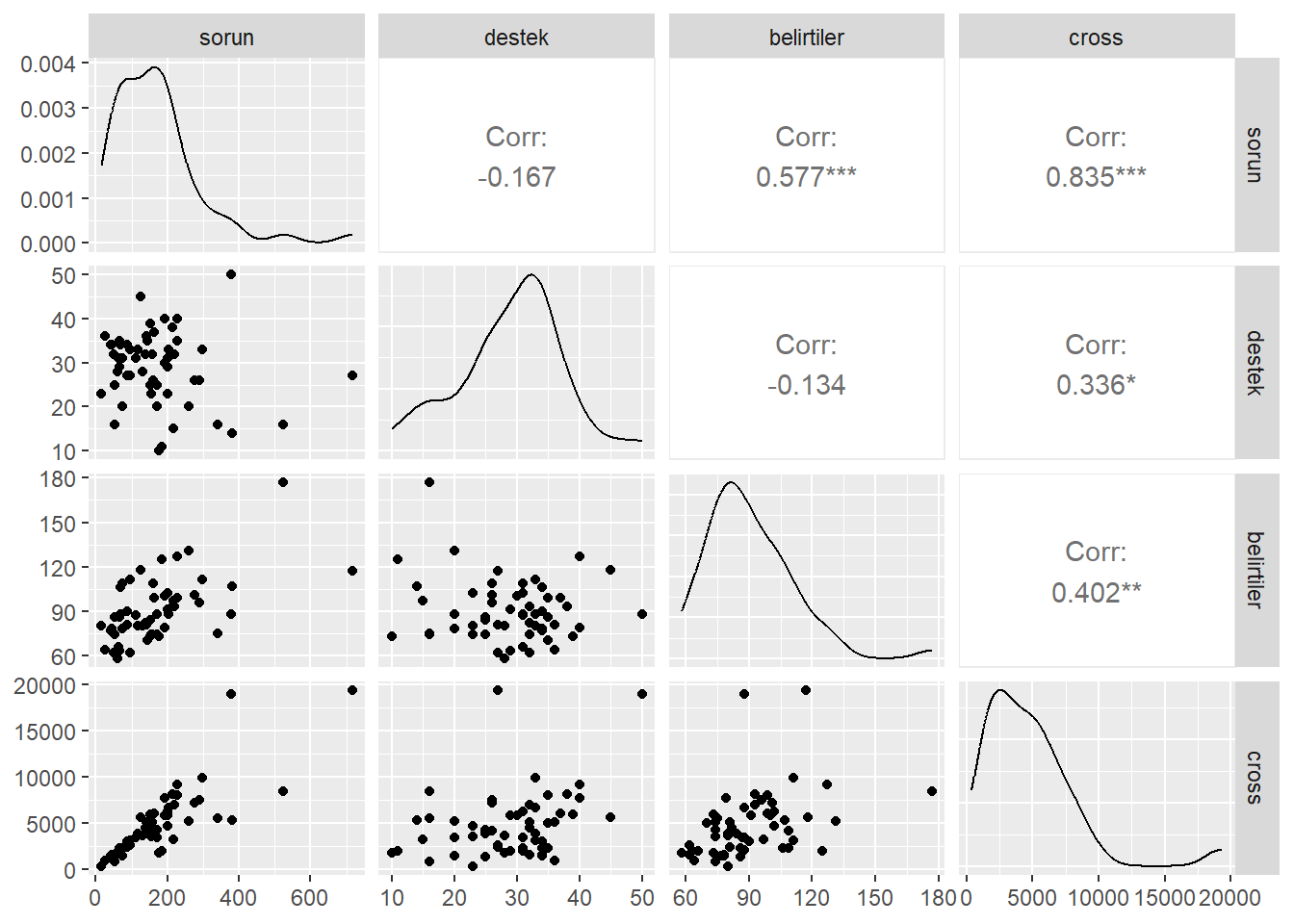

ggpairs(zorluklar[,c(5,6,4,8)])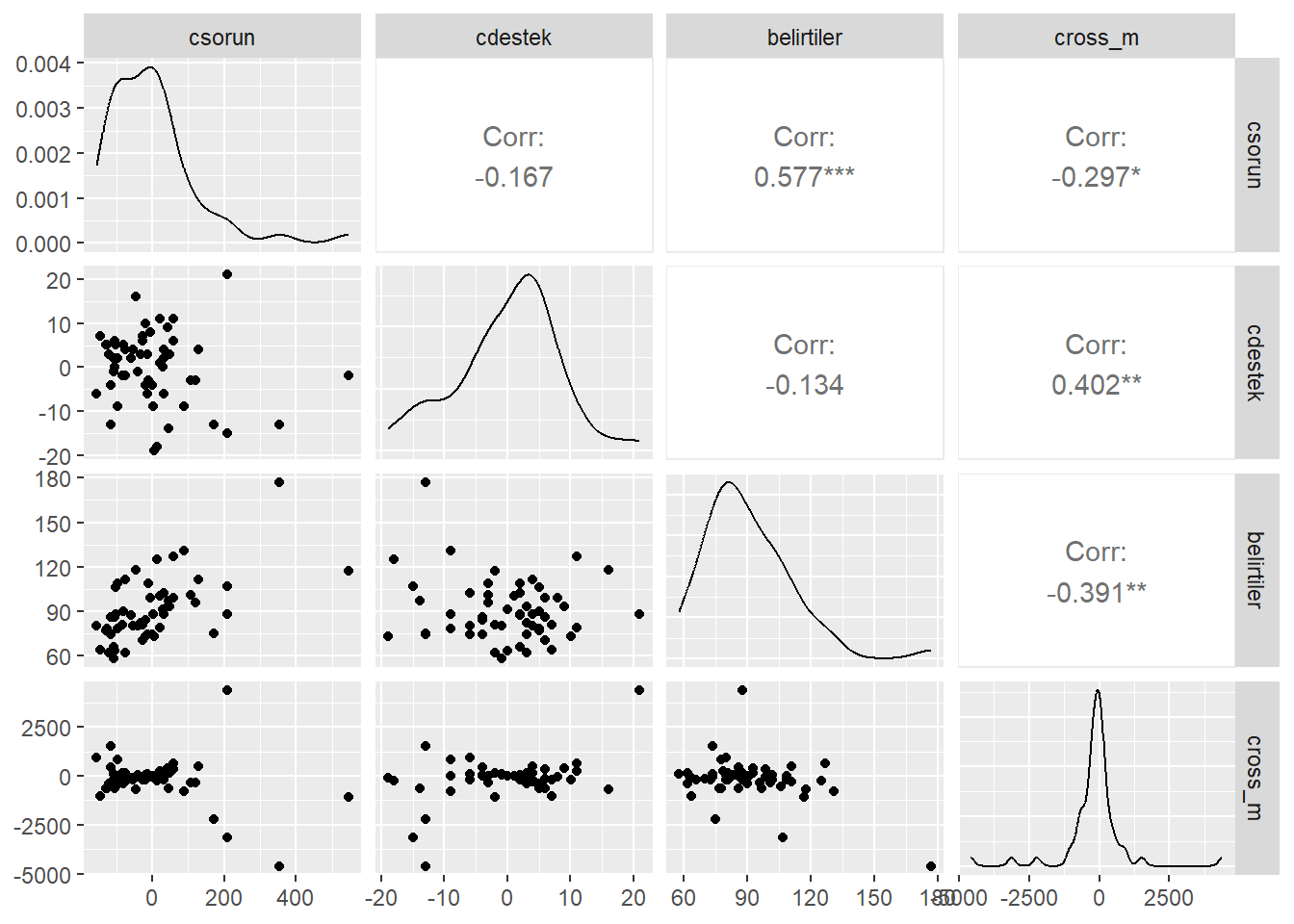

Belirtilerin bağımlı degişken, merkezlenen sorunların ve merkezlenen desteğin bağımsız değişken olarak modellendiğ regresyonda, iki bağımsız değişkenin etkileşimini incelemek üzere etkileşim terimi de regresyon modeline eklenir.

n_model <- lm(belirtiler  ~ csorun  + cdestek  ,data=zorluklar)
cross_model <- lm(belirtiler  ~ csorun  + cdestek + cross_m ,data=zorluklar)

etkileşim teriminin açıklanan varyansı ne kadar değiştirdiğine bakalım.

glance(n_model)$r.squared

[1] 0.3344622

glance(cross_model)$r.squared

[1] 0.3884955

Etkileşimli modelin daha yüksek bir $R^2$ değerine sahip olduğu açıktır. Bununla birlikte birden fazla açıklayıcı değişkene sahip modellerde model seçimi için $R^2$ iyi bir fikir değildir, çünkü herhangi bir değişken moda eklendiğinde $R^2$ artar.
model seçimi için (daha) objektif bir ölçü düzeltilmiş $R^2$ dir, modele dahil edilen değişken sayısı için bir düzeltme uyguladığından, yeni değişken herhangi bir yeni bilgi sağlamıyorsa veya tamamen ilgisizse düzeltilmiş $R^2$ artmaz. Bu da düzeltilmiş $R^2$ çoklu regresyon modellerinde model seçimi için tercih edilebilir bir metriktir.
etkileşim teriminin düzeltilmiş $R^2$ yi ne kadar değiştirdiğine bakalım.

glance(n_model)$adj.r.squared

[1] 0.3093475

glance(cross_model)$adj.r.squared

[1] 0.3532164

tidy(cross_model)

Hem merkezlenen sorun hem de etkileşim terimi istatistiksel olarak anlamlıdır (sırasıyla p ˂ 0.001 ve p = 0.037). Ancak merkezlenen destek istatistiksel olarak anlamlı değildir (p = 0.634). Destek değişkeni etkileşim teriminin hesaplanmasında yer aldığından, regresyon modelinde kalabilir.

mod1 <- lm(belirtiler  ~ csorun*cdestek  ,data=zorluklar)

interactions::interact_plot(mod1, "csorun", modx = "cdestek")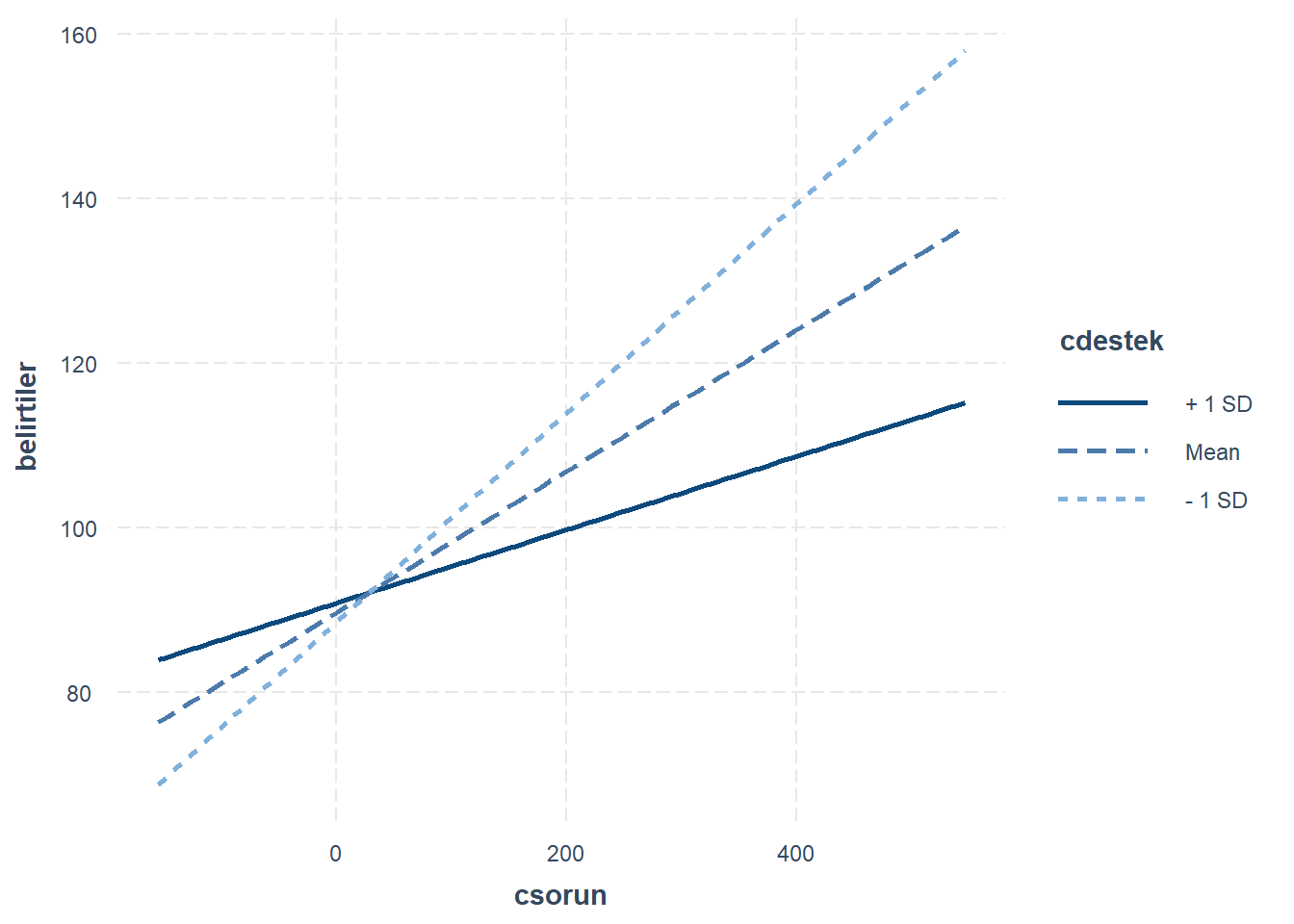

Etkileşim etkisinin anlamını yorumlamak için değişkenler arasındaki ilişkilerin grafik ile gösterimi yardımcı olabilir. En basit çözüm sosyal desteğin sabit düzeyleri için zorluklar ve psikolojik belirtiler arasındaki ilişkiye bakmaktır.
Merkezlenen sosyal destek değişkeninin değerileri -21 ile +19 arasında değişmektedir. Bu değişken için düşük, orta ve yüksek değerleri temsil etmek üzere sırasıyla -15, 0 ve +15 değerleri seçilebilir.

library(dplyr)
zorluklar <- zorluklar %>% mutate(
  cdestek_kat = case_when(
  cdestek <= -15 ~ "dusuk",
  cdestek >-15 &    cdestek <15~ "orta",
  cdestek >=15 ~ "yuksek",
  )
)
zorluklar <- zorluklar %>%  arrange(csorun)

yüksek düzeyde sosyal destek ile sorunlardaki artışlar psikolojik belirtilerde küçük artışlarla ilişkilendirilirler. Orta düzeyde sosyal destek ile sorunlardaki artışlar psikolojik belirtilerde daha büyük artışlarla ilişkilendirilir. Düşük düzeyde sosyal destek ile sorunlardakı artışlar psikolojik belirtilerde dramatik artışlarla ilişkilendirilir.

24 Etkilesim Etkisi

Etkileşim etkisini strargazer paketi ile gösterelim.

library(stargazer)


stargazer(n_model, cross_model, type = "text", title = "Düzenleyici Etkisi")


Düzenleyici Etkisi
=================================================================
                                 Dependent variable:             
                    ---------------------------------------------
                                     belirtiler                  
                             (1)                    (2)          
-----------------------------------------------------------------
csorun                     0.096***               0.086***       
                           (0.019)                (0.019)        
                                                                 
cdestek                     -0.098                 0.146         
                           (0.293)                (0.305)        
                                                                 
cross_m                                           -0.005**       
                                                  (0.002)        
                                                                 
Constant                  90.429***              89.585***       
                           (2.333)                (2.292)        
                                                                 
-----------------------------------------------------------------
Observations                  56                     56          
R2                          0.334                  0.388         
Adjusted R2                 0.309                  0.353         
Residual Std. Error    17.457 (df = 53)       16.893 (df = 52)   
F Statistic         13.317*** (df = 2; 53) 11.012*** (df = 3; 52)
=================================================================
Note:                                 *p<0.1; **p<0.05; ***p<0.01

Etki büyüklüğünün incelenmesi de oldukça önemlidir. Düzenleyicilik etki analizini hesaplamada genellikle Cohen f^2 kullanılır ve küçük, orta, büyük olarak değerlendirmede .005 , .01, .025 kesme değerleri kullanılır (Aguinis vd., 2015; Kenny, 2018)

library(effectsize)
cohens_f_squared(cross_model)

library(rockchalk)
ps  <- plotSlopes(mod1, plotx="csorun", modx="cdestek", xlab = "Sorun", ylab = "Belirtiler", modxVals = c("std.dev"))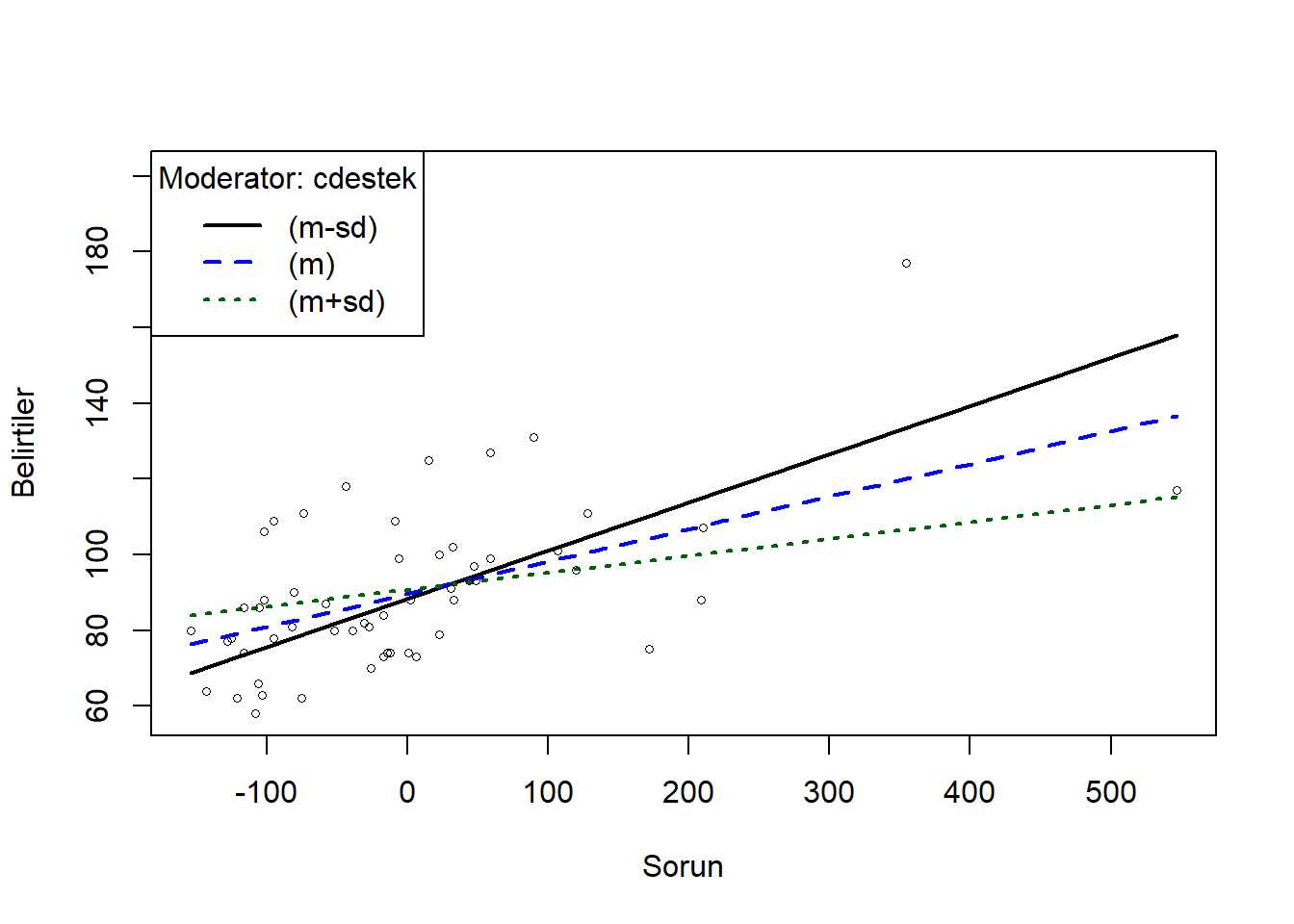

library(car)
avPlots(mod1)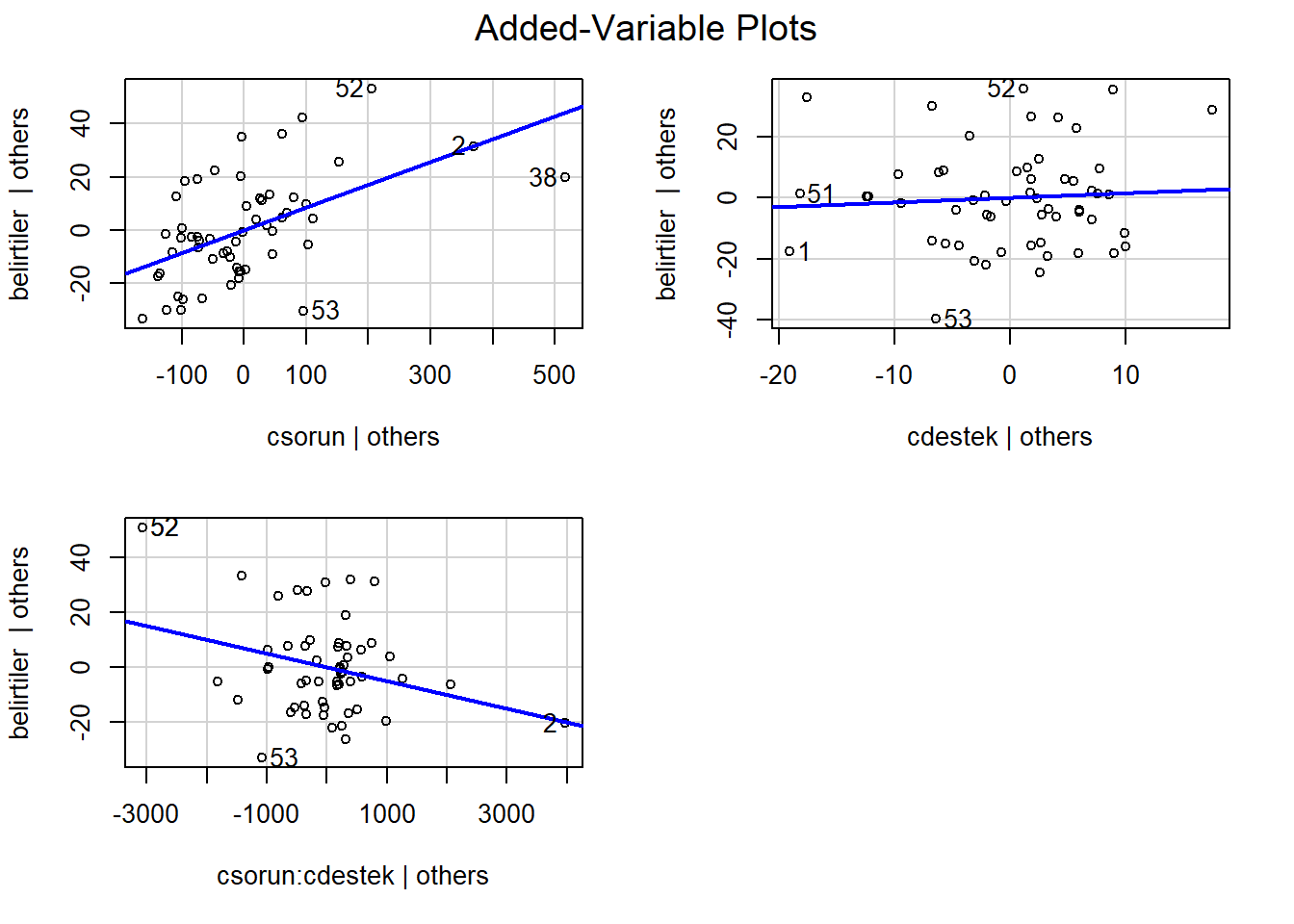

25 Düzenleyicilik Analizi - II

Bu örnekte, bir yüksek lisans öğrencisinin aldığı uyku saati sayısı (X) ile bu derse verdiği dikkat (Y) arasındaki ilişkinin kahve tüketiminden (Z) etkilenip etkilenmediğini inceleyeceğiz. Burada bağımlı değişken (Y), bağımsız değişken (X) ve düzenleyici değişken (Z) seviyelerinin çarpımı haline getirerek düzenleyici etkisi yaratıyoruz. emo::ji("link") duzenleyici.Rds

duzenleyici <- readRDS("data/duzenleyici.Rds")
summary(duzenleyici)

       X                X1                Z               Y          
 Min.   : 0.195   Min.   :  1.597   Min.   :15.95   Min.   :  2.386  
 1st Qu.: 4.025   1st Qu.: 35.967   1st Qu.:25.75   1st Qu.: 30.155  
 Median : 6.247   Median : 53.225   Median :30.29   Median : 47.761  
 Mean   : 6.483   Mean   : 56.806   Mean   :30.96   Mean   : 47.763  
 3rd Qu.: 8.767   3rd Qu.: 74.035   3rd Qu.:36.11   3rd Qu.: 61.727  
 Max.   :14.749   Max.   :157.231   Max.   :48.34   Max.   :136.947

Moderasyon, düzenleyici değişken (Z) ile bağımsız değişken (X) arasında anlamlı etkileşimler aranarak test edilebilir. Özellikle, çoklu bağlantıyı azaltmak ve yorumlamayı kolaylaştırmak için hem düzenleyici hem de bağımsız değişkeni merkezlemek gereklidir. Merkezleme, bir değişkenin ortalamasını o değişkendeki her değerden çıkararak yapılabilir.

#C Merkezleme
attach(duzenleyici)
Xc    <- c(scale(X, center=TRUE, scale=FALSE)) #uyku saati
Zc    <- c(scale(Z,  center=TRUE, scale=FALSE)) # moderator; kahve tuketimi

R’deki bir dizi paket, QuantPsyc paketinin moderate.lm() fonksiyonu ve pequod paketi de dahil olmak üzere, düzenleyici analizlerini yürütmek ve çizmek için de kullanılabilir. Ancak, burada gösterildiği gibi bunu geleneksel çoklu regresyon kullanarak yapmak da kolaydır ve bu paketlerdeki temel analiz (düzenleyici ve bağımsız etkileşimi) bu yaklaşımla aynıdır. Burada kullanılan rockchalk paketi, R’de bulunan birçok grafik ve çizim paketinden biridir ve özellikle regresyon analizlerinde kullanılmak üzere tasarlandığı için seçilmiştir.

attach(duzenleyici)
fitMod <- lm(Y ~ Xc + Zc + Xc * Zc) 
coef(summary(fitMod))

              Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 48.5444271 1.17285613 41.389925 5.149708e-63
Xc           5.2081205 0.34870152 14.935755 8.862490e-27
Zc           1.1044337 0.15537153  7.108340 2.077645e-10
Xc:Zc        0.2338362 0.04134056  5.656338 1.592946e-07

Sonuçlar normal çoklu regresyon sonuçlarına benzer şekilde sunulmuştur. Bu modelde önemli etkileşim etkisi anlamlı olduğu için, bağımsız değişken veya düzenleyici değişken etkilerini ayrı yorumlamaya gerek yoktur.

library(stargazer)
stargazer(fitMod,type="text", title = "Uyku ve Kahvenin Dikkate Etkisi")


Uyku ve Kahvenin Dikkate Etkisi
===============================================
                        Dependent variable:    
                    ---------------------------
                                 Y             
-----------------------------------------------
Xc                           5.208***          
                              (0.349)          
                                               
Zc                           1.104***          
                              (0.155)          
                                               
Xc:Zc                        0.234***          
                              (0.041)          
                                               
Constant                     48.544***         
                              (1.173)          
                                               
-----------------------------------------------
Observations                    100            
R2                             0.766           
Adjusted R2                    0.759           
Residual Std. Error      11.647 (df = 96)      
F Statistic           104.784*** (df = 3; 96)  
===============================================
Note:               *p<0.1; **p<0.05; ***p<0.01

Elle modelimiz, uyunan saatler ile kahve tüketimi arasında bu derse verilen dikkat üzerinde anlamlı bir etkileşim olduğunu göstermektedir (b = .23, SE = .04, p < .001). Uyku ve kahve tüketimi derse verilen dikkat üzerindeki değişkenliği %76.6’sını açıklamaktadır.

cohens_f_squared(fitMod)

Etkileşim etki büyüklüğünün oldukça büyük olduğu bulunmuştur. Fakat etkileşim etkisinin ne anlama geldiği hakkında daha iyi bir fikir edinmek için bu etkileşimi görsel olarak vermek daha iyi olacaktır.

rockchalk paketi plotSlopes() fonksiyonu otomatik olarak ılımlı etkinin basit eğimlerini (ortalamanın 1 SD üstü ve 1 SD altı) çizecektir.

#Plotting
library(rockchalk)
ps  <- plotSlopes(fitMod, plotx="Xc", modx="Zc", xlab = "Uyku", ylab = "Verilen Dikkat", modxVals = "std.dev")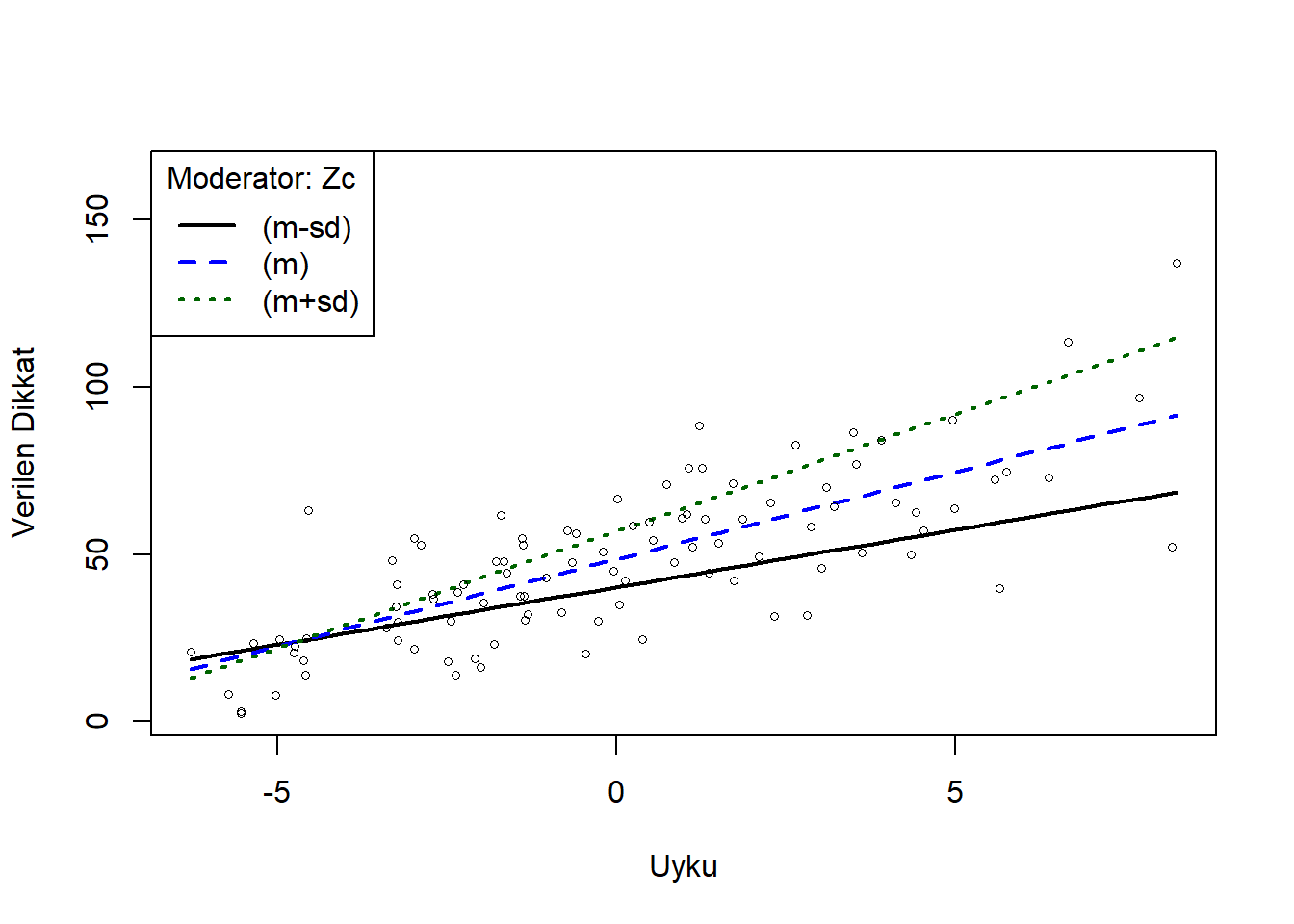

Bu şekil, daha az kahve içenlerin (ortalamanın 1 sd altında olanlar-siyah çizgi) dün gece ne kadar çok uyurlarsa o kadar çok dikkat ettiklerini, ancak genel ortalamada daha az dikkat ettiklerini göstermektedir (mavi çizgi). Daha fazla kahve içenler (ortalamanın 1 sd üstünde olanlar-yeşil çizgi) daha fazla uyuduklarında da daha fazla dikkat etmiş ve ortalamadan daha fazla dikkat göstermişlerdir. Ortalamadan 1 sd daha az kahve içenlerin uyku saatleri arttıkça verilen dikkatleri de artmaktadır. Daha fazla veya daha az kahve içenlerin eğimlerindeki fark, kahve tüketiminin uyku saatleri ile dikkat arasındaki ilişkiyi ılımlı hale getirdiğini göstermektedir.

library(car)
avPlots(fitMod)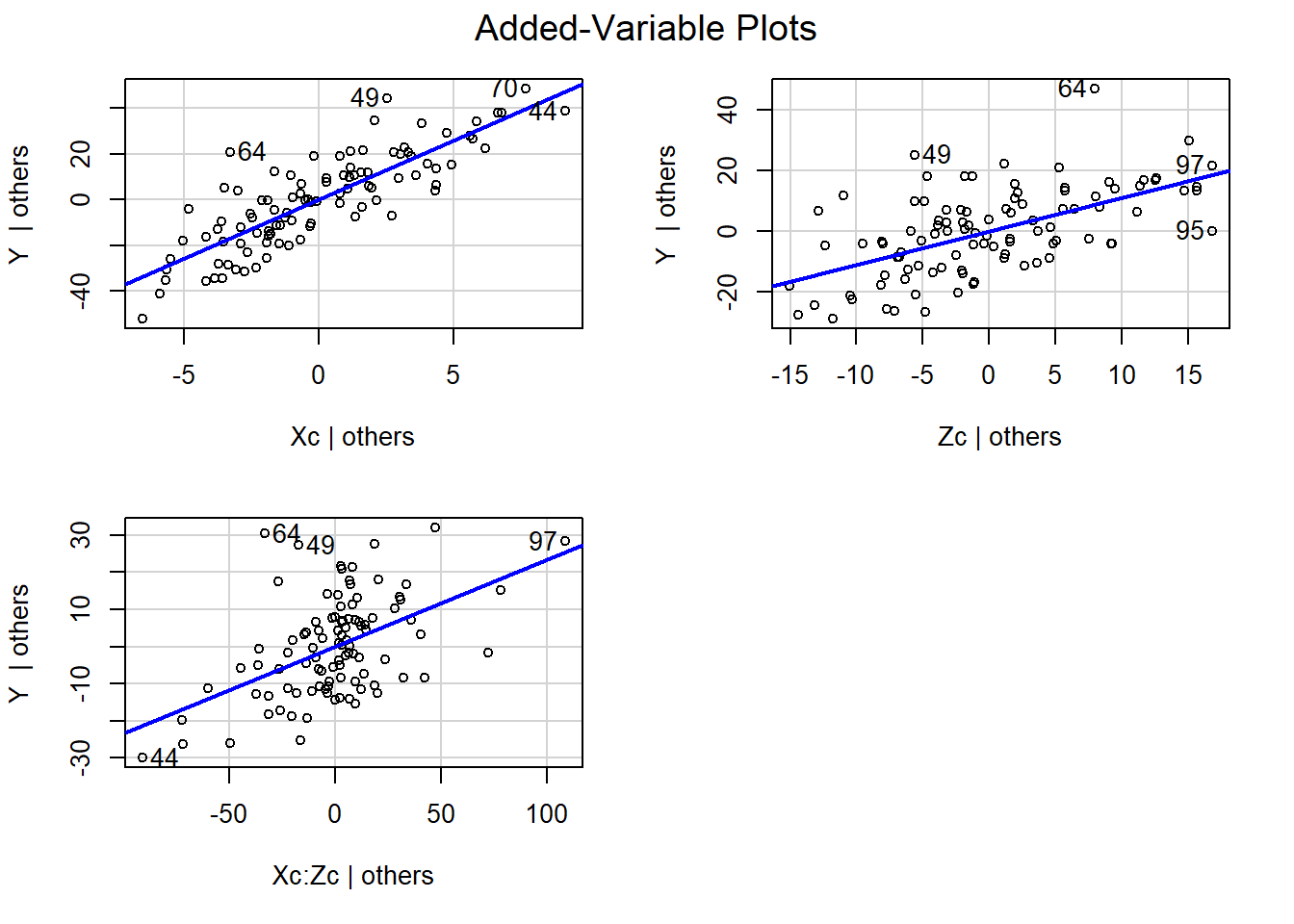

26 Önemli Notlar

Düzenleyici değişken mutlaka literatüre göre seçilmelidir.
Bağımlı değişkenin düzenleyici etkisinin olamayacağı açıklanmalıdır (çünkü matematiksel formül aynı)
Düzenleyici etki anlamlı çıktığında bu etkileşim görselleştirilmeli, anlamlı çıkmazsa buna gerek duyulmamalı. Hatta bu değişken modelden bile çıkarılıp, sadece regresyon analizi yapılabilir.
Merkezileştirme ve standartlaştırmaya gerek olmayabilir. Zaten bu işlemler etkileşim etkisi üzerinde herhangi bir değişime neden olmaz.
Örneklem büyüklüğü yeterli olmalı ve örneklemin evreni temsil gücü yüksek olmalıdır.
Düzenleyici değişken sürekli ya da kategorik olabilir fakat sürekli değişkenin kategorik değişkene dönüştürülmesi pek tercih edilmemelidir (edilirse bir kesme değer, ortalama vb. ile belirlenmeli)
Bağımsız değişken sürekli ya da kategorik olabilir. Bağımlı değişken de aynı şekilde fakat kategorik olduğunda lojistik regrosyon veya probit regresyon ile hesaplama yapılmalıdır.

27 Causal Quartet

Causal Quartet, Anscombe’un Dörtlüsü’ne benzer şekilde, iki değişken arasındaki ilişkiyi görselleştirmenin önemini vurgulamak için oluşturulmuş bir veri setidir.
Ancak, Causal Quartet, değişkenler arasındaki nedensel ilişkileri incelemek için tasarlanmıştır.
Causal Quartet, dört farklı veri seti içerir ve her biri farklı bir nedensel ilişkiyi temsil eder. Bu veri setleri, değişkenler arasındaki ilişkilerin karmaşıklığını ve nedenselliğin önemini vurgulamak için kullanılır.

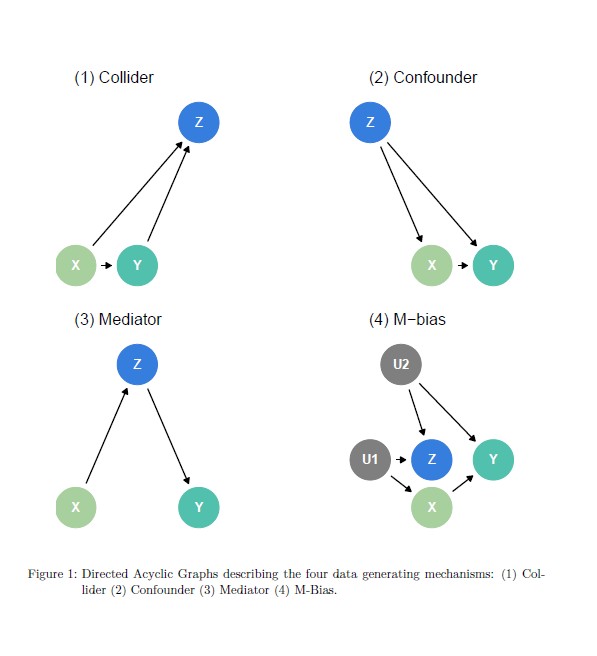
27.1 Collider (Çarpıştırıcı) Örneği

Problem:
Bir hastane, COVID-19 ölüm oranını analiz ederken yalnızca hastaneye yatan hastaların verilerini kullanmaktadır.

Değişkenler:

X: COVID-19 şiddeti (hafif / şiddetli)

Y: Ölüm

Z: Hastaneye yatış (Collider)

Neden Sorun?
Hem COVID-19 şiddeti (X) hem de ölüm riski (Y), hastaneye yatış (Z) ile ilişkilidir.
Yalnızca hastaneye yatırılan vakalar analiz edildiğinde, şiddetli vakalardaki ölüm oranı olduğundan düşük görünebilir. Çünkü hafif vakaların büyük bir kısmı hastaneye yatmadığı için veriye dahil edilmemiştir.
Bu durum, COVID-19 şiddeti ve ölüm arasındaki gerçek ilişkiyi çarpıtabilir.

Çözüm:
Collider değişkeni üzerinde kontrol yapılmamalı; bunun yerine, tüm popülasyonu temsil eden bir veri seti kullanılmalıdır.

Bir değişken, iki farklı değişkenin sonucu ise (yani iki değişkenin birleşim noktası ise) buna collider denir.

İki değişken, aynı değişkeni neden olur (ikisi de ona doğru ok çıkar).
Genellikle bir analizde collider üzerinde kontrol yapmak ters etki yaratır ve iki değişken arasında yapay bir ilişki oluşmasına neden olur.
(Yani normalde ilişkili olmayan iki değişken, sanki ilişkiliymiş gibi görünür.)
Ama Collider üzerinde kontrol edersen, X ile Z yapay olarak ilişkili görünmeye başlar.

X: Spor yapma

Z: Sağlıklı beslenme

Collider: Vücut formu

→ Spor yapma da sağlıklı beslenme de vücut formunu etkiler.
→ Eğer sadece “iyi vücut formuna sahip olanları” seçersen, bu iki şey (spor ve sağlıklı beslenme) sanki birbiriyle ilişkilidir gibi görünür.
→ Halbuki popülasyonda normalde spor yapmakla sağlıklı beslenmek arasında doğrudan bir ilişki olmayabilir.

Terim	Tanım
Collider	İki değişkenin etkilediği bir üçüncü değişkendir; bu değişken üzerinde kontrol yapıldığında, iki değişken arasında yapay bir ilişki oluşur.

27.2 Confounder (Karıştırıcı) Örneği

Problem: Kahve tüketimi (X) ile akciğer kanseri (Y) arasında pozitif bir korelasyon bulunuyor.

Değişkenler:

X: Kahve tüketimi,
Y: Akciğer kanseri,
Z: Sigara içmek (Confounder).

Neden Sorun?:

Sigara içenler (Z) hem daha fazla kahve tüketir (X) hem de akciğer kanseri riski taşır (Y).
Kahve ve kanser arasında sahte bir ilişki oluşur.

Çözüm:

Sigara içme durumu (Z) için düzeltme yapılmalı.

27.3 Confounder vs Collider

Özellik	Confounder (Bozucu Değişken)	Collider
Yapı	Üçüncü değişken, hem X’i hem Y’yi etkiler.	Üçüncü değişken, X ve Y’nin etkilediği ortak sonuçtur.
Şema	Confounder → X Confounder → Y	X → Collider ← Y
X ve Y Arasında Doğal İlişki	Confounder varsa, X ve Y zaten ilişkili görünür (aslında ilişkili olmayabilir).	Collider varsa, X ve Y bağımsızdır.
Kontrol Etmenin Etkisi	Confounder’ı kontrol etmek ilişkiyi temizler (gerçek ilişkiyi gösterir).	Collider’ı kontrol etmek yapay ilişki üretir (olmayan bir ilişki varmış gibi görünür).
Örnek	- X: Sigara içme - Y: Akciğer kanseri - Confounder: Asbest maruziyeti	- X: Spor yapma - Y: Sağlıklı beslenme - Collider: Vücut formu

Confounder → İki değişkeni birbirine bağlayan sebep.

Collider → İki değişkenin sonucu.

27.4 Mediator (Aracı Değişken) Örneği

Problem: Egzersiz (X) ile kalp sağlığı (Y) arasındaki ilişkiyi inceleyen bir çalışma.

Değişkenler:

X: Egzersiz,
Z: Kilo kaybı (Mediator),
Y: Kalp hastalığı riski.

Analiz Seçenekleri:

Toplam Etki: Egzersizin kalp sağlığına tüm etkisi (kilo kaybı dahil).
Model: Y∼X (sonuç: egzersiz riski azaltır).
Doğrudan Etki: Egzersizin kilo kaybı haricindeki etkisi (örneğin, kas güçlenmesi).
Model: Y∼ X+Z (sonuç: egzersizin direkt etkisi sıfır çıkabilir).

Neden Önemli?:

Kilo kaybını (Z) düzeltirseniz, egzersizin farklı mekanizmalarını izole edersiniz.

27.5 M-Bias (M-Yanılgısı) Örneği

Problem: Bir eğitim çalışmasında, sosyoekonomik statü (Z) için düzeltme yapılıyor, ancak bu değişken ölçülmeyen faktörlerden etkileniyor.

Değişkenler:

U1 : Ailenin eğitim geçmişi (ölçülmüyor),
U2 : Okulun kaynakları (ölçülmüyor),
Z: Ölçülen “aile geliri” (M-Bias kaynağı),
X: Eğitim programı,
Y: Test puanları.

Neden Sorun?:

Z (aile geliri), U1 ve U2 tarafından etkilenir.
Z için düzeltme yapmak, programın (X) etkisini olduğundan farklı gösterir.

Çözüm:

M-Bias’tan kaçınmak için önemli confounder’ları doğrudan ölçmeye çalışın (örneğin, okul kaynakları).

Özetle:

Collider: “Gözlemlediğiniz veri kümesi, bir seçilim yanlılığı içeriyor olabilir mi?”
Confounder: “İlişkinin arkasında gizli bir ortak neden var mı?”
Mediator: “Etkiyi hangi mekanizma üzerinden ölçmek istiyorum?”
M-Bias: “Düzeltme yaptığım değişken, ölçülmeyen faktörlerle bağlantılı mı?”

library(tidyverse)
library(quartets)
ggplot(causal_quartet, aes(x = exposure, y = outcome)) +
  geom_point() + 
  geom_smooth(method = "lm", formula = "y ~ x") +
  facet_wrap(~dataset)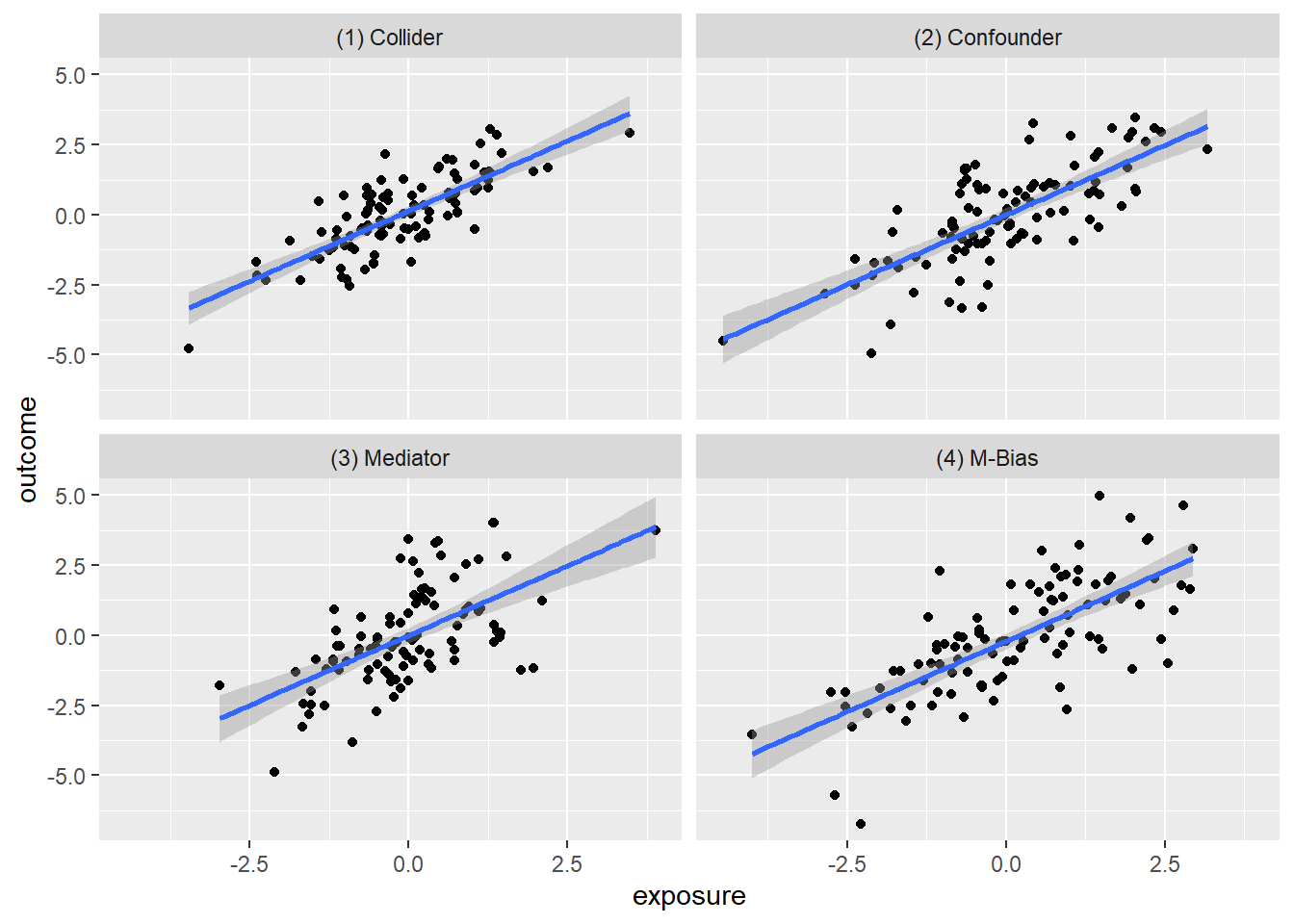

causal_quartet |>
  nest_by(dataset) |>
  mutate(`Y ~ X` = round(coef(lm(outcome ~ exposure, data = data))[2], 2),
         `Y ~ X + Z` = round(coef(lm(outcome ~ exposure + covariate, data = data))[2], 2),
         `Correlation of X and Z` = round(cor(data$exposure, data$covariate), 2)) |>
  select(-data, `Data generating mechanism` = dataset) |>
  knitr::kable()

Data generating mechanism	Y ~ X	Y ~ X + Z	Correlation of X and Z
(1) Collider	1	0.55	0.7
(2) Confounder	1	0.50	0.7
(3) Mediator	1	0.00	0.7
(4) M-Bias	1	0.88	0.7

Basit regresyonda ($Y \sim X$) hepsi 1 idi.

Ama Z’yi denkleme ekleyince ($Y \sim X + Z$) işler karıştı:

Mediator: Etki kocaman bir 0’a düştü!
- “Zincirleme Reaksiyon” X, Z sayesinde Y’yi etkiliyor. Ne Yapmalıyız? Eğer X’in toplam etkisini merak ediyorsak Z’yi KONTROL ETMEMELİYİZ.
Confounder: Etki 0.5’e düştü (Yarı yarıya).
- “Klasik Ortak Sebep” Z hem X’i hem Y’yi etkiliyor. Ne Yapmalıyız? Z’yi KONTROL ETMELİYİZ.
Collider: Etki 0.55 oldu.
- “Seçim Yanlılığı” Hem X hem Y, Z’nin olmasına sebep oluyor. Ne Yapmalıyız? Z’yi KONTROL ETMEMELİYİZ.
M-Bias: Etki 0.88 oldu.

27.5.1 “Sinsi Tuzak” Genellikle Z’yi kontrol etmemeliyiz.

27.5.2 Kaynaklar

Wagner, B. M., Compas, B. E., & Howell, D. C. (1988). Daily and major life events: A test of an integrative model of psychosocial stress. American Journal of Community Psychology, 16 (2), 189-205.
Baron, R., & Kenny, D. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51, 1173-1182.
Hayes, A. F. (2022). Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach (Vol. 3). The Guilford Press.
Hlavac, Marek (2022). stargazer: Well-Formatted Regression and Summary Statistics Tables. R package version 5.2.3. https://CRAN.R-project.org/package=stargazer
Tingley, D., Yamamoto, T., Hirose, K., Keele, L., & Imai, K. (2014). Mediation: R package for causal mediation analysis.

https://nicolarighetti.github.io/mediation-moderation-and-conditional-process-analysis-with-r/moderation.html#moderation-with-multicategorical-variables

https://bookdown.org/mike/data_analysis/moderation.html

https://cran.r-project.org/web/packages/rempsyc/vignettes/moderation.html

https://rpubs.com/cbwin/r4ps8_med-and-mod

1 Regresyon Kullanım Alanları

2 Regresyon Kullanım Alanları

3 Basit Doğrusal Regresyon

4 En küçük kareler yöntemi

5 Kestirimin Standart Hatası

5.1 Basit Doğrusal Regresyon Uygulama

6 Bağımsız değişkenler arasındaki ilişki

7 Uygulama

8 Çoklu korelasyon katsayısı

9 Belirlilik Katsayısı

10 Kestirimin standart hatası

11 Model veri uyumu

12 Kaygının sabit tutulması

13 Motivasyonun sabit tutulması

14 Regresyon Sabiti

15 Standart puanlar ile regresyon

16 Yordanan ve Artık Değerler

16.1 Yordanan ve Artık Değerlerin Standart Puanları

17 Model Grafikleri

18 Çoklu Regresyon

19 Yol Şeması

20 Aşamalı (Stepwise) Regresyon

21 Etkili Gözlemlerin Belirlenmesi

22 Kategorik Bağımsız bir Değişken ile Çoklu Regresyon

22.1 Dummy Değişkenlerin Oluşturulması Örnek: Performansın Yordanması

23 Çoklu Regresyonda İki-Yönlü Etkileşim Etkisi

24 Etkilesim Etkisi

25 Düzenleyicilik Analizi - II

26 Önemli Notlar

27 Causal Quartet

27.1 Collider (Çarpıştırıcı) Örneği

27.2 Confounder (Karıştırıcı) Örneği

27.3 Confounder vs Collider

27.4 Mediator (Aracı Değişken) Örneği

27.5 M-Bias (M-Yanılgısı) Örneği

27.5.1 “Sinsi Tuzak” Genellikle Z’yi kontrol etmemeliyiz.

27.5.2 Kaynaklar